Feladat: 665. matematika feladat Korcsoport: 16-17 Nehézségi fok: átlagos
Megoldó(k):  Makkai Mihály ,  Pintér László ,  Szabados József ,  Szabó Endre 
Füzet: 1955/november, 95 - 97. oldal  PDF  |  MathML 
Témakör(ök): Háromszögek hasonlósága, Síkgeometriai számítások trigonometria nélkül háromszögekben, Alakzatok köré írt kör, Feladat
Hivatkozás(ok):Feladatok: 1955/február: 665. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás: Legyen az adott háromszög AB és AC oldala egy Σ(α) rendszer két tengelye. (A Σ(a) rendszertől l. Gönyei A. cikkét a K. M. L. 1955. januári számában). Fel fogjuk írni egyrészt a háromszög köré írt kör K középpontja és adjungáltjára vonatkozó

ζ+ψ=90∘(1)
összefüggést, majd felírjuk ugyanezt az összefüggést a háromszög M magassági pontjára és ennek adjungáltjára, mely a talpponti háromszög M2M3 oldala.
K pont adjungáltja a háromszög BC-vel párhuzamos középvonala, ezért (1) ebben az esetben azt adja, hogy (l. ábra)
ζ1+γ=90∘,vagyisζ1=90∘-γ.(2)
 
1. ábra
 

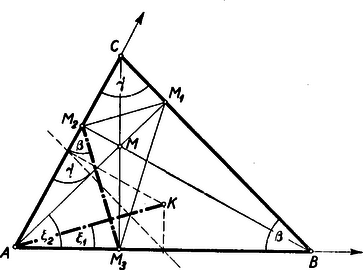A magassági pontra és adjungáltjára az (1) szögösszefüggés így alakul:
ζ2+AM2M3∢=90∘,
de az AM1B derékszögű háromszögből ζ2+β=90∘, így AM2M3∢=β, és következőleg az AM2M3▵,-ből AM3M2∢=γ.
Viszont (2) szerint a KAM∢=ζ1=90∘-γ, ebből következik, hogy
AK⊥M2M3.

Tompaszögű háromszög esetén a bizonyítás ugyanígy elvégezhető. Ha a háromszög derékszögű, akkor a talpponti háromszög az átfogóhoz tartozó magassággá fajul, és így az egyik oldaláról nem tehet beszélni.
 

Szabó Endre (Gyöngyös, Vak Bottyán g. IV. o. t.)
 

Természetesen a Σ(a) rendszer felhasználása nélkül is könnyen bizonyítható a feladat állítása, amint azt az alábbi megoldások mutatják, melyek mind hegyes-, mind tompaszögű háromszög esetén egyaránt érvényesek.
 

II. megoldás: A betűzést a 2. ábra mutatja.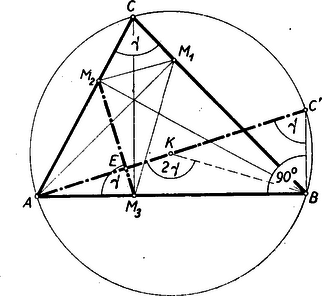
 
 
2. ábra
 

Thales tétele értelmében a BC fölé, mint átmérő fölé, rajzolt félkör átmegy az M2 és M3 pontokon, tehát BCM2M3 húrnégyszög, és így az M2M3A∢, mint külső szög egyenlő a szemközti belső szöggel, vagyis
M2M3A∢=γ.

Másrészt, ha a körülírt körben A átellenes pontját C'-vel jelöljük, akkor a keletkezett ABC' háromszögben a Thales-tétel alapján az ABC'∢ derékszög, a kerületi szögek tétele szerint pedig AC'B∢=γ, és így
C'AB∢=90∘-γ.

AC' és M2M3 metszéspontját E-vel jelölve, az AEM3 háromszög két szögének összege γ+(90∘-γ)=90∘, és így a harmadik szög
AEM3∢=90∘,
ami bizonyítandó volt.
 

Szabados József (Bp. III, Árpád g. III. o. t.)
 

III. megoldás: Az AKB∢ (2. ábra), mint középponti szög egyenlő 2γ-val, tehát a
KAB∢≡EAM3∢=180∘-2γ2=90∘-γ.

Mint ismeretes, a talpponti háromszög oldalai által lemetszett háromszögek hasonlók az eredeti háromszöghöz (a szögek egyenlősége már az I. osztályos tankönyvben megtalálható), vagyis
AM3M2∢=γ,
tehát az AEM2▵ harmadik szöge 90∘.
 

Makkai Mihály (Bp. V., Eötvös g. II. o. t.)
 

IV. megoldás: Ismeretes tétel, hogy az M pont bármely háromszögoldalra vonatkozó tükörképe rajta van a körülírt körön. Tehát M'' és M''' (3. ábra) a körülírt körön van és M2M=M2M'', M3M=M3M''' miatt
M''M'''∥M2M3.(1)
 
 
3. ábra
 

Elég tehát azt megmutatni, hogy M''M''' merőleges az AK egyenesre. Mivel előbbi szakasz húrja a K középpontú körülírt körnek, az állítás következik abból, ha megmutatjuk, hogy A felezi a kör M''M''' ívét. Mivel pedig az AM'' és AM''' távolságok az AM távolság tükörképei, s így a fölöttük levő ívek is egyenlők, tehát A valóban felezi az M''M''' ívet, ebből pedig következik a bizonyítandó állítás.
 

Pintér László (Celldömölk, Gábor Áron g. IV. o. t.)