Kezdőlap


Feladat:	664. matematika feladat	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Daróczy Zoltán
Füzet:	1955/november, 94 - 95. oldal		PDF \| MathML
Témakör(ök):	Szélsőérték-feladatok differenciálszámítás nélkül, Négyszögek szerkesztése, Szögfüggvények, síkgeometriai számítások, Feladat
Hivatkozás(ok):	Feladatok: 1955/február: 664. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás: Megoldhatjuk feladatunkat számítással. Egy tetszés szerinti, a feltételeknek megfelelő egyenlő szárú trapéz szárának hosszát jelöljük $x$ -szel. A trapézek $x$ -től függő $t (x)$ területe ‐ ha $α < 90^{\circ}$ ‐ egy téglalapra és két derékszögű háromszögre bontható (1. ábra):

1. ábra

\begin{matrix} t (x) = (d - 2 x) x sin α + x^{2} sin α cos α = (sin α cos α - 2 sin α) x^{2} + (d sin α) x ., \end{matrix}

(A képlet

α \geq 90^{\circ}

-ra is helyesen adja a területet, mert ekkor a második tag 0 ill. negatív.)
Ez

x

-re nézve másodfokú függvény, melyben a négyzetes tag együtthatója

sin α (cos α - 2) < 0

, mert az első tényező az

0 < α < 180^{\circ}

intervallumban pozitív, a második tényező pedig negatív.
Tehát a

t (x)

függvénynek az

\begin{matrix} x_{0} = \frac{- d sin α}{2 sin α (cos α - 2)} = \frac{d}{2 (2 - cos α)} \end{matrix}

helyen maximuma van.
Eszerint az

x_{0}

szár a

\begin{matrix} (2 - cos α) : \frac{d}{2} = 1 : x_{0} \end{matrix}

aránypárból, negyedik arányosként megszerkeszthető (2. ábra).

2. ábra

\begin{matrix} α = 90^{\circ} esetén x = \frac{d}{4}, \end{matrix}

vagyis a trapéz téglalappá válik, amelynek oldalai

\frac{d}{4}

és

\frac{d}{2}

Daróczy Zoltán (Debrecen, Ref. g. Ill. o. t.)

II. megoldás: A feladatot tisztán geometriai úton is megoldhatjuk. Ha egy ‐ a terület maximális voltán kívül ‐ a feltételeknek megfelelt trapézt a párhuzamos oldalak felezőpontján átmenő egyenessel kettévágunk, akkor olyan derékszögű trapézt kapunk, amelyben a ferde szár és az egyik párhuzamos oldal összege

\frac{d}{2}

, a másik párhuzamos oldalon pedig (a derékszögön kívül)

α

nagyságú szög van. Ezek közül kell tehát a legnagyobb területűt meghatároznunk.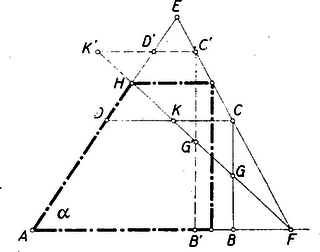

3. ábra

Legyen

A B C D

egy kívánt tulajdonságú trapéz (3. ábra). Hosszabbítsuk meg az

A D

ferde szárát a

D E = D C

távolsággal. Tehát

A E = \frac{d}{2}

. Messe

E C

A B

egyenest

F

-ben. Ekkor nyilván az összes kívánt tulajdonságú trapézek

A

-val átellenes csúcsai az

E F

szakaszra esnek. Rajzoljuk meg a

B C

merőleges szár

G

felezőpontját. Az összes ilyen felezőpontok egy

F

-ből induló egyenesen sorakoznak. Messe ez az egyenes

A E

-t

H

-ban, az

A B C D

trapéz

C D

oldalát vagy annak meghosszabbítását

K

-ban. A

G C K

háromszöget

G

-re tükrözve, látjuk, hogy az

A B C D

trapéz területe a

D H K

háromszög területével kisebb az

A F H

háromszög területénél. Így a legnagyobb területű trapézt úgy kapjuk, hogy a

H

pontból párhuzamost húzunk

A F

-fel és ennek

E F

-fel való metszéspontjából merőlegest bocsátunk

A F

-re.
Az eljárás egyformán érvényes, ha

α

hegyesszög, derékszög vagy tompaszög.

Megjegyzés: Néhány megoldó úgy vélte a szerkesztést elvégezhetőnek, hogy tetszőleges sugarú körben megszerkesztette a maximális területű

α

szögű egyenlő szárú trapézt és azután ‐ az adott

d

-nek megfelelően ‐ ehhez hasonló, kisebb vagy nagyobb trapézt szerkesztett. Természetesen ez nem helyes, mert ilyen módon arra az esetre oldotta meg a feladatot, hogy

α

mellett

α

köré írt kör sugara állandó. Ez esetben azonban a szár változtatásával a

d

is változik, amint a kitűzött feladatban ‐ midőn

d

állandó ‐ a szár változtatásával a trapéz köré írt körének sugara változik.