Feladat: 657. matematika feladat Korcsoport: 16-17 Nehézségi fok: átlagos
Megoldó(k):  Bonyhárd Péter ,  Dominyák Imre ,  Heinemann Zoltán ,  Makkai Mihály ,  Surán Gábor 
Füzet: 1955/november, 85 - 87. oldal  PDF  |  MathML 
Témakör(ök): Egyenesek egyenlete, Egyenes, Feladat
Hivatkozás(ok):Feladatok: 1955/január: 657. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás: Nem megy az általánosság rovására, ha koordináta-rendszerünk x tengelyéül a g egyenest, y tengelyéül pedig az l egyenest választjuk (1. ábra).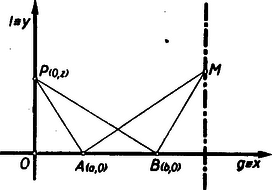

 
 
1. ábra
 

Az A pont koordinátái: (a,0), a B ponté: (b,0), a P ponté: (0,z). Ha a, vagy b valamelyike, pl. a=0 (azaz A éppen a két adott egyenes metszéspontja), akkor a kérdéses mértani hely egyetlen ponttá fajul el; ez a pont B.
A továbbiakban tegyük fel, hogy a és b egyike sem 0, és egyelőre zárjuk ki a z=0 esetet (P ne legyen az origóban).
Az AP egyenes iránytangense: -za; a BP egyenes iránytangense: -zb, tehát az A pontban AP-re emelt merőleges és a B-ben BP-re emelt merőleges egyenes egyenlete:
y=az(x-a)ésy=bz(x-b)

Az egyenletrendszert megoldva, nyerjük az M metszéspont koordinátáit
x=a+b,y=abz.(1)
z minden értékéhez (z=0-t kizártuk!) tartozik egy koordináta értékpár. Miután pedig x független z-től, az M pontok egy, az y tengellyel párhuzamos, egyenesen helyezkednek el, melynek egyenlete
x=a+b.

Hátra van még annak eldöntése, hogy az (1) egyenletrendszerrel jellemzett egyenes minden pontja hozzátartozik-e a mértani helyhez. Tekintve, hogy y=abz szerint az egyenes minden pontjának y ordinátájához (y=0 kivételével) tartozik egy z(=aby) érték, ezzel együtt tartozik egy P pont is az y tengelynek választott l egyenesen. Az eddig kizárt z=0 esetet úgy értelmezhetjük, mint amelynek az (1) egyenes végtelen távoli pontja felel meg, míg az l egyenes végtelen távoli pontjához az (1) egyenes y=0-hoz tartozó pontját gondolhatjuk megfeleltetve. Ezzel a kiterjesztéssel most már mondhatjuk, hogy a keresett mértani hely a teljes x=a+b egyenes vagyis az az egyenes, mely l-lel tükrös helyzetű az AB szakasz felezőpontjára nézve.
 

Bonyhárd Péter (Bp. VIII., Apáczai Csere g. IV. o. t.)
 

II. megoldás: Jelöljük g és l metszéspontját 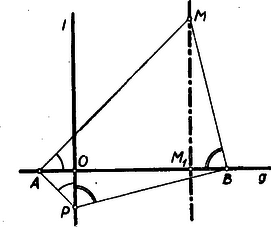O-val.
 
 
2. ábra
 

Az MAP▵ és MBP▵ derékszögű, tehát Pythagoras tétele alapján (2. ábra)
AM2+AP2=MP2=BM2+BP2,
azaz
AM2-BM2=BP2-AP2.De  BP2=OP2+OB2,AP2=OP2+OA2,  és ígyAM2-BM2=(OP2+OB2)-(OP2+OA2)=OB2-OA2=állandó.

Azonban ismeretes (lásd K. M. L. 423. sz. feladat megoldását 1952 okt. 47. old.), hogy azon pontok mértani helye a síkban, amelyeknek két adott ponttól mért távolságai négyzeteinek különbsége állandó: egy egyenes, amely az adott pontok összekötésére merőleges.
 

Dominyák Imre (Miskolc, Földes F. g. IV. o. t.)
 

III. megoldás: Tetszőleges P-hez tartozó M pontból g-re bocsátott merőleges talppontját M1-gyel (2. ábra) jelölve, két pár hasonló derékszögű háromszög keletkezik:
MM1A▵∼AOP▵ésMM1B▵∼BOP▵,
mert az ábrán egyformán jelölt szögek merőleges szárú szögek.
A megfelelő oldalak aránya egyenlő:
MM1M1A=AOOP(1)MM1M1B=BOOP(2)


(1)-et elosztva (2)-vel, nyerjük, hogy
M1BM1A=AOBO=konstans(3)

Miután M1, helyzete nem függ a P ponttól, az M pontok mértani helye az M, ponton átmenő, g-re merőleges egyenes. (3) szerint az M pont O-nak az AB szakasz felezőpontjára vonatkozó tükörképe.
Az M1M egyenes minden pontja hozzátartozik a mértani helyhez, mert minden M-hez megtalálhatjuk az l egyenesen azt a P pontot, amelyből létrejött (ugyanazzal a szerkesztéssel, amellyel a P-ből nyerjük az M-et).
 

Heinemann Zoltán (Pécs, Bányaip. techn. II o. t.)
 

IV. megoldás: ABMP (3. ábra, ill. AMBP ‐ 2. ábra) húrnégyszög, mert A-ból és B-ből a PM szakasz derékszög alatt látszik.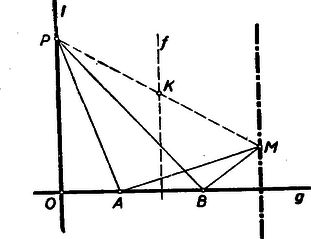
 
 
3. ábra
 

Thales tétele alapján PM a köréírt kör átmérője, K középpontja pedig az AB szakaszt merőlegesen felező f egyenesen van (f∥l). Az M pont tehát mindenkor a P pont tükörképe az f egyenesen mozgó K pontra nézve, vagyis az M pontok mértani helye az l egyenesnek f-re vonatkozó tükörképe.
 

Makkai Mihály (Bp. V., Eötvös g. II. o. t.)
 

V. megoldás: Szerkesszük meg az APB▵ H magassági pontját (4. ábra).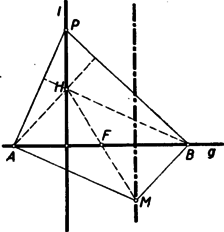
 
 
4. ábra
 

Az AHBM négyszög paralelogramma, mert a szerkesztés szerint az egyik oldalpárja AP-re, a másik oldalpárja pedig BP-re merőleges. A paralelogramma középpontja az AB szakasz F felezőpontja. Az F pontra nézve M és H tükrös helyzetű. Ha P végigfut az l egyenesen, l állandóan az APB▵ magasságvonala marad, tehát a H magasságpontok mértani helye az l egyenes, s így az M pontok mértani helye az AB szakasz felezőpontjára nézve l-lel tükrös helyzetű egyenes.
 

Surán Gábor (Bp. V., Eötvös g. III. o. t.)