| Feladat: | 652. matematika feladat | Korcsoport: 16-17 | Nehézségi fok: átlagos |
| Megoldó(k): | Csiszár Imre | ||
| Füzet: | 1955/október, 52 - 53. oldal |  PDF | PDF |  MathML MathML |
|
| Témakör(ök): | Hossz, kerület, Feladat | ||
| Hivatkozás(ok): | Feladatok: 1954/december: 652. matematika feladat | ||
|
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. Kárteszi Ferenc Egy különös geometria című cikkében (KML IX. köt. 3 ‐ 4 szám, 71. o.) bebizonyítja, hogy a végtelen sakktáblán egy mezőről kiindulva az lóugrással elérhető mezők elhelyezkedése szabályos, mégpedig ezek éppen az -ik és -ik övben helyezkednek el. E tétel segítségével a feladatot úgy oldjuk meg, hogy megszámoljuk az -ik és -ik egyesített öv jelzésű négyzeteit, azaz az lóugrással elérhető mezőket. 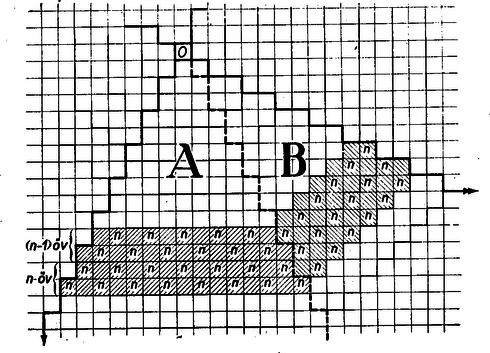 Osszuk fel a vizsgálandó konfiguráció-negyedet az ábrán látható két részre. Vizsgáljuk előbb az -val jelölt részt. Az -edik öv külső sora mezőből áll, és e sornak két szélső mezője mindig jelzésű. Ebből következik, hogy az -edik öv külső és belső, továbbá az -edik öv külső és belső sorában rendre , , , számú jelzésű mező van. Tehát a negyed-konfiguráció és -edik egyesített övének jelzésű része A jelzésű részben az -nel jelölt mezők az -edik és -edik övben 3 egyenlő hosszú, párhuzamos átlón helyezkednek el, mégpedig az -edik övben mindig a két szélső és az -edik övben a középső átlón. Mivel az -edik övben a középső átló , a két szélső átló pedig mezőből áll azért a -vel jelölt részben az -nel jelölt mezők száma 3 . Az és rész -nel jelölt mezőinek együttes száma tehát Az egész konfiguráció -nel jelölt, vagyis pontosan lóugrással elérhető mezőinek száma (ha );
|