| Feladat: | 650. matematika feladat | Korcsoport: 16-17 | Nehézségi fok: átlagos |
| Megoldó(k): | Legéndy Károly , Mestyán Anna | ||
| Füzet: | 1955/május, 151 - 152. oldal |  PDF | PDF |  MathML MathML |
|
| Témakör(ök): | Szabályos testek, Térelemek és részeik, Feladat | ||
| Hivatkozás(ok): | Feladatok: 1954/december: 650. matematika feladat | ||
|
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. I. megoldás: 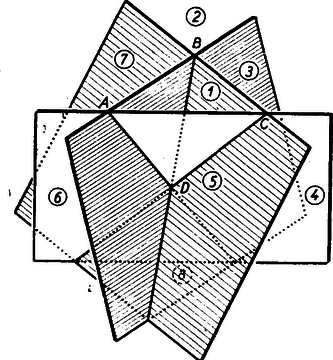 b) Az tetraéder egyik lapjának síkja (pl. az jelöletlen, tiszta sík) a teret 2 részre bontja, egy másik lap síkja (pl. a sűrűn vonalkázott ) az előbbi 2 térrész mindegyikét kettéosztja, tehát a két egymást metsző sík 4 térrészt határol. A harmadik sík (a ritkán vonalkázott ) az eddig létrejött mindegyik térrészt kettéosztja, miután az első két sík egyikével sem párhuzamos, és a két sík metszés vonalán sem megy át. A három sík tehát 8 térrészt határol, amint az ábra mutatja. A negyedik sík (), melyet külön nem szemléltettünk, minden eddig keletkezett térrészt két részre vág, kivéve a 8-cal jelzettet, melyet a tetraéder csúcsához tartozó csúcstriéder határol. Így összesen térrész keletkezik, melyek közül csak az az egy véges, amelyet a tetraéder tölt ki.
II. megoldás: Ha a kocka belsejében fekvő tetszőleges pontot összekötjük a kocka egyik csúcsával, akkor ez a csúcsban találkozó 3 sík átmetszésével (vagyis a kérdéses csúcson áthaladva) olyan térrészbe jut, amelyet az említett 3 sík határol, és ebben a térrészben benne is marad, mert újabb síkot nem metsz; tehát a kocka minden csúcsához egy végtelen térrész csatlakozik. Ha a kocka belsejében fekvő pontból a kocka egyik élét merőlegesen metsző egyenest indítunk, akkor ez az egyenes az élnek, vagyis az élben találkozó két síknak az átmetszése után olyan térrészbe jut, melynek két határoló síkja az élben találkozó két kockalap síkja. Ez a térrész is végtelen, mert az él átmetszése után az egyenes újabb síkot már nem metsz. Végül a kocka belsejében fekvő pontból állítsunk merőlegest az egyik kockalapra; ez az egyenes egyetlen lap átmetszése után jut bele egy végtelen térrészbe. Tekintve, hogy a csúcshoz csatlakozó térrészbe 3 sík átmetszése után jutottunk, míg az élhez csatlakozó térrészbe csak 2 sík átmetszése után, e két térrész nem lehet azonos. Két határoló síkjuk lehet közös (ha a csúcs éppen rajta van a kérdéses élen), de még akkor is elválasztja őket az a sík, amelyet nem metszettünk át, amikor az élhez csatlakozó térrészbe jutottunk. Éppígy belátható, hogy a laphoz csatlakozó térrész is különbözik az előző kettőtől. Miután pedig a csúcshoz csatlakozó térrészek száma megegyezik a csúcsok számával, az élhez csatlakozóké az élek számával, a laphoz csatlakozóké a lapok számával, az összes térrészek száma: végtelen véges térrész, vagyis összesen 27 térrész. Szemléletünk mutatja, hogy a megszámlált térrészek az egész teret kitöltik, tehát az említett módon valóban megszámláltuk az összes térrészt. b) A tetraéder esetében az előbbihez teljesen hasonló gondolatmenettel arra jutunk, hogy a térrészek száma .
Megjegyzés: A II. megoldásban közölt megszámlálás után nem fölösleges megvizsgálni, hogy a kérdéses térrészek kitöltik-e az egész teret. (Lásd jelen számunkban a 690. feladatot). |