Kezdőlap


Feladat:	646. matematika feladat	Korcsoport: 18-	Nehézségi fok: átlagos
Megoldó(k):	Bausz Imre , Kismarty Loránd
Füzet:	1955/május, 145 - 147. oldal		PDF \| MathML
Témakör(ök):	Mértani sorozat, Szögfüggvények, síkgeometriai számítások, Feladat
Hivatkozás(ok):	Feladatok: 1954/december: 646. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás: Legyenek a körök sugarai rendre 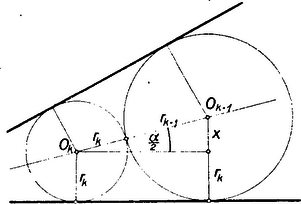$r_{1}$ , $r_{2}, ..., r_{k}$ , $r_{k + 1}, ..., r_{n}$ .
$r_{k}$ ismeretében a rákövetkező kör $r_{k + 1}$ sugara kiszámítható. A betűzést az 1. ábra mutatja.

1. ábra

\begin{matrix} r_{k + 1} = r_{k} + x = r_{k} + O_{k} O_{k + 1} sin \frac{α}{2} = \\ = r_{k} + (r_{k} + r_{k + 1}) sin \frac{α}{2}, \end{matrix}

vagyis

\begin{matrix} r_{k + 1} - r_{k + 1} sin \frac{α}{2} = r_{k} + r_{k} sin \frac{α}{2}, \end{matrix}

és így

\begin{matrix} r_{k + 1} = r_{k} \frac{1 + sin \frac{α}{2}}{1 - sin \frac{α}{2}}, ahol k = 1,2, ..., n - 1. \end{matrix}

r_{1}

r_{2}, ..., r_{n}

sugarak tehát mértani sorozatot alkotnak, amelynek hányadosa

q = \frac{1 + sin \frac{α}{2}}{1 - sin \frac{α}{2}}

.
A keresett terület tehát

\begin{matrix} T = t_{1} + t_{2} + ... + t_{n} = π (r_{1}^{2} + r_{2}^{2} + ... + r_{n}^{2}) . \end{matrix}

Az előbbiek alapján a zárójelben álló kifejezés olyan mértani sorozat, amelynek első tagja

r_{1}^{2}

és hányadosa

{(\frac{1 + sin \frac{α}{2}}{1 - sin \frac{α}{2}})}^{2}

. A mértani sorozat összegképletét felhasználva

\begin{matrix} T = r_{1}^{2} π \frac{{(\frac{1 + sin \frac{α}{2}}{1 - sin \frac{α}{2}})}^{2 n} - 1}{{(\frac{1 + sin \frac{α}{2}}{1 - sin \frac{α}{2}})}^{2} - 1} . \end{matrix}

Kismarty Loránd (Pannonhalma, Bencés g. I. o. t.)

II. megoldás: Az

\frac{r_{k + 1}}{r_{k}} = q

n

-től független, állandó viszonyszám másképpen is meghatározható. A két szomszédos kör közös

T

érintőpontjában megrajzolt közös érintő messe a szög egyik szárát

F

-ben. A betűzést a 2. ábra mutatja.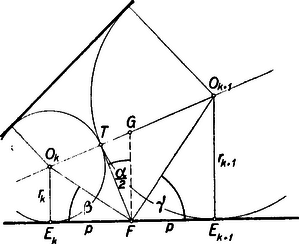

2. ábra

F

-ben a szögszárra emelt merőlegesnek a centrális egyenessel való metszéspontja legyen

G

. A

T F G ∢

, mint merőleges szárú szög egyenlő

\frac{α}{2}

-vel. A

T F E_{k} ∢

, ill.

T F E_{k + 1} ∢

felezőjének az

E_{k} E_{k + 1}

szögszárral bezárt szögét

β

-val, illetőleg

γ

-val jelölve, nyilván

\begin{matrix} β = \frac{90^{\circ} - \frac{α}{2}}{2} = 45^{\circ} - \frac{α}{4} és γ = \frac{90^{\circ} + \frac{α}{2}}{2} = 45^{\circ} + \frac{α}{4} . \end{matrix}

Legyen

F T = F E_{k} = F E_{k + 1} = p

, akkor

\begin{matrix} r_{k} & = F E_{k} \cdot tg β = p \cdot tg (45^{\circ} - \frac{α}{4}), \\ r_{k + 1} & = F E_{k + 1} \cdot tg γ = p \cdot tg (45^{\circ} + \frac{α}{4}), \end{matrix}

és így

\begin{matrix} \frac{r_{k + 1}}{r_{k}} = q = \frac{tg (45^{\circ} + \frac{α}{4})}{tg (45^{\circ} - \frac{α}{4})} . \end{matrix}

q

ezen alakjával a területek összege

\begin{matrix} T = r_{1}^{2} π \frac{\frac{{tg}^{2 n} (45^{\circ} + \frac{α}{4})}{{tg}^{2 n} (45^{\circ} - \frac{α}{4})} - 1}{\frac{{tg}^{2} (45^{\circ} + \frac{α}{4})}{{tg}^{2} (45^{\circ} - \frac{α}{4})} - 1} = \\ = r_{1}^{2} π \frac{{tg}^{2 n} (45^{\circ} + \frac{α}{4}) - {tg}^{2 n} (45^{\circ} - \frac{α}{4})}{{tg}^{2 (n - 1)} (45^{\circ} - \frac{α}{4}) [{tg}^{2} (45^{\circ} + \frac{α}{4}) - {tg}^{2} (45^{\circ} - \frac{α}{4})]} \end{matrix}

alakban adódik.

Bausz Imre (Sopron, Széchenyi g. IV. o. t.)

Megjegyzés: A

q

utóbbi értékét az I. megoldásban nyert értékből közvetlenül is megkaphatjuk, ha az

1 + sin \frac{α}{2} = sin 90^{\circ} + sin \frac{α}{2} = 2 sin \frac{90^{\circ} + \frac{α}{2}}{2} cos \frac{90^{\circ} - \frac{α}{2}}{2} = 2 sin (45^{\circ} + \frac{α}{4}) cos (45^{\circ} - \frac{α}{4})

és

1 - sin \frac{α}{2} = 2 cos (45^{\circ} + \frac{α}{4}) sin (45^{\circ} - \frac{α}{4})

helyettesítést végezzük el.