| Feladat: | 644. matematika feladat | Korcsoport: 16-17 | Nehézségi fok: nehéz |
| Megoldó(k): | Bártfai P. , Biczó G. , Bonyhárd P. , Csiszár I. , Darvas I. , Fuchs T. , Harza T. , Jónás J. , Kálmán Gy. , Katona P. , Katz T. , Kiss P. , Legéndy K. , Lőke Mária , Mecseki A. , Pasitka B. , Pátkai Gy. , Quittner P. , Rázga T. , Stáhl J. , Szabados József , Szabó E. , Szeidl T. , Zsombok Z. | ||
| Füzet: | 1955/május, 143 - 144. oldal |  PDF | PDF |  MathML MathML |
|
| Témakör(ök): | Hossz, kerület, Pitagoraszi számhármasok, Feladat | ||
| Hivatkozás(ok): | Feladatok: 1954/november: 644. matematika feladat | ||
|
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. I. megoldás: Feladatunk így is fogalmazható: , , egész számok alkothatnak-e pitagoraszi számhármast? 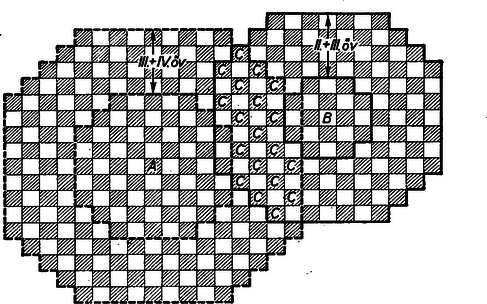 Ha kimutatjuk, hogy van olyan mező a konfigurációban, melyre ezen megjelölés során és is került, a feladatot nyilván megoldottuk. Kimutatjuk, hogy ilyen mező van. A mezőtől lóugrásnyira levő mezők az és -ik egyesített övben helyezkednek el (és ha , akkor csakis ott), hasonlóan az mezőtől lóugrásnyira levő mezők a és -ik egyesített övben vannak. Minthogy Az általánosság megszorítása nélkül feltehetjük, hogy sötét mező. Természetesen a két öv valamennyi közös mezője nem felel meg a feladat feltételeinek. A megfelelő mezők kiválasztása ‐ az előbbi feltétel kihasználásával ‐ a következő módon történhet: Ha páros és és páratlan, akkor szintén sötét mező, és ‐ akár az , akár a mezőtől vett távolságot tekintjük ‐ világos mező, tehát a két öv közös részének valamennyi világos mezeje megfelel a feladat feltételeinek: Ha páratlan, akkor világos mező és sötét, ha páros és páratlan (lásd ábránkat), ill. világos ha páratlan és páros. Ábránk a , és esetet tünteti fel. Szabados József (Bp. III., Árpád g. III. o. t.) II. megoldás: Tekintsük a , és speciális pitagoraszi számhármasokat. Legyen a végtelen sakktábla kiindulási mezeje. Az -tól számított -ik övben csupa és számmal jelölt mező van. Tehát a és mezők ebben az övben vannak és különböző színűek, mert és különböző párosságú. Tehát páratlan, és így lehet . Mivel , azért a -ik övben tetszőlegesen kiválasztott ponthoz mindig található (az I. megoldás alapján) az övben fekvő pont, melyre nézve tényleg . Triviális példa: esetén a -ik övben csupa 4-gyel és 5-tel jelölt mező található (lásd 1954. novemberi 3‐4. szám 73. old. 2. ábra) és bármelyik két szomszédos és távolsága .
|