| Feladat: | 640. matematika feladat | Korcsoport: 16-17 | Nehézségi fok: átlagos |
| Megoldó(k): | Dancs Mária , Pesti András , Rázga Tamás , Szeidl Béla | ||
| Füzet: | 1955/április, 117 - 119. oldal |  PDF | PDF |  MathML MathML |
|
| Témakör(ök): | Trapézok, Síkgeometriai számítások trigonometria nélkül négyszögekben, Feladat | ||
| Hivatkozás(ok): | Feladatok: 1954/november: 640. matematika feladat | ||
|
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. E feladat igen termékenynek bizonyult. Nagyon sokféle megoldás érkezett be. Legtöbbnyire a cosinus-tételt használták fel a megoldók (többféleképpen is), de több másfajta megoldás között szerepelt az összefüggés, ahol az átlók felezőpontjainak egymástól való távolsága, valamint a súlyvonal hosszát megadó azonosság , lásd 510. sz. feladatot, VI. köt. 88. old. 1953. nov.) is. A sokféle megoldásból az alábbi hármat választottuk ki, mint a legegyszerűbbeket és a legfrappánsabbakat. Ezek közül a legegyszerűbb a tétel általánosítását is lehetővé teszi. I. megoldás: A betűzést az 1. ábra mutatja. 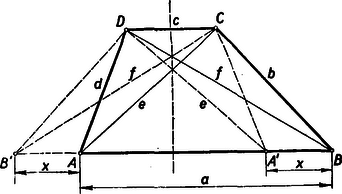 Az egyik párhuzamos (pl. a ) oldalt merőlegesen felező egyenesre tükrözzük az és szárakat, nyerjük az , ill. egyenlőszárú trapézeket. Ezen egyenlőszárú trapézekre, mint húrnégyszögekre, alkalmazva Ptolemaios tételét
II. megoldás: Ismeretes, hogy egy csúcsból kiinduló két háromszögoldal bármelyikéből és a második oldalnak az előbbi oldalon levő merőleges vetületéből alkotott egy-egy téglalap területe egyenlő . Ez igaz akár hegyes-, akár tompa-, akár derékszöget zár be a két oldal. (Utóbbi esetben mindkét téglalap területe külön-külön .) Ilyen módon bármely háromszögnek mind a három csúcspontjánál keletkezik 2‐2 ilyen egyenlő területű téglalap. Alkalmazzuk e tételt trapézünk (2. ábra) és (3. ábra) háromszögére. Mindkét ábrában az egyenlő területű téglalapokat ugyanazzal a római számmal jelöltük. és . 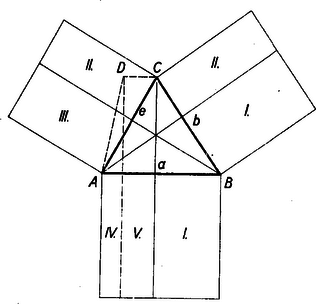 A 2. ábrán az előbbiek alapján 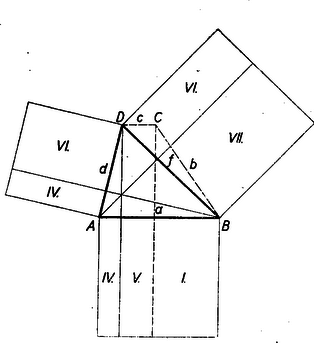 A 3. ábrán Tehát
III. Megoldás: Pythagoras-tétele is elegendő tételünk bizonyításához, sőt általánosításához is. Húzzuk meg a és pontokból a trapéz magasságát. 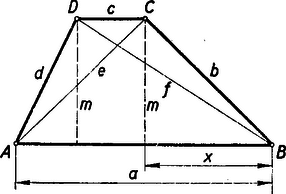 A betűzést a 4. ábra mutatja. A jobboldalon az első zárójelben levő kifejezés értéke (5) alapján , a második zárójelben levő kifejezés értéke (6) alapján , és így Megjegyzés: Megmutatjuk, hogy általános négyszögben A bizonyítás az előbbihez hasonló. 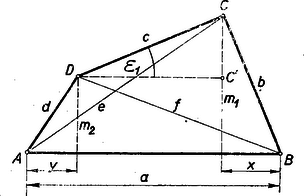 A betűzést az 5. ábra mutatja.
() és () összege Hurkolt négyszög esetén helyébe annak kiegészítő szöge lép. Hurkolt trapéz esetén, miatt,
|