Kezdőlap


Feladat:	639. matematika feladat	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Bittsánszky Géza
Füzet:	1955/április, 116. oldal		PDF \| MathML
Témakör(ök):	Simson-egyenes, Feladat
Hivatkozás(ok):	Feladatok: 1954/november: 639. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Jelöljük a körülírt kör $P$ pontjából az oldalakra bocsátott merőlegesek talppontját $U$ , $V$ , $W$ -vel. A szerkesztés és Thales-tétele alapján $P B U V$ (1. ábra) és $P U C W$ (2. ábra) húrnégyszögek.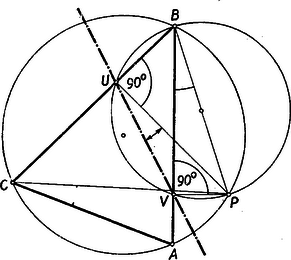
Be fogjuk bizonyítani, hogy $P U V ∢ = P U W ∢$ , tehát az ábráinkban szaggatottan rajzolt $U V$ egyenes egybeesik az $U W$ egyenessel. Ez azonban azt jelenti, hogy $U$ , $V$ és $W$ egy egyenesbe esik.

1. ábra

Az 1. ábránkból látható, hogy

\begin{matrix} P U V ∢ = P B V ∢, \end{matrix}

mint közös

\hat{P V}

ívhez tartozó kerületi szögek.
Hasonlóképpen

\begin{matrix} P B V ∢ \equiv P B A ∢ = P C A ∢, \end{matrix}

mint közös

\hat{A P}

íven nyugvó kerületi szögek, és így

\begin{matrix} P U V ∢ = P C A ∢ . \end{matrix}

(1)

2. ábra

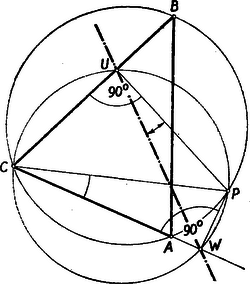A 2. ábránkban

\begin{matrix} P C A ∢ \equiv P C W ∢ = P U W ∢, \end{matrix}

(2)

mint közös

\hat{P W}

íven nyugvó kerületi szögek.
(1) és (2)-ből következik, hogy

\begin{matrix} P U V ∢ = P U W ∢, \end{matrix}

amivel tételünket bebizonyítottuk.

Bittsánszky Géza (Bp. VIII., Piarista g. I. o. t.)