Kezdőlap


Feladat:	635. matematika feladat	Korcsoport: 18-	Nehézségi fok: átlagos
Megoldó(k):	Bánhidy K. , Bártfai P. , Beke Gy. , Beliczky G. , Benkő B. , Béres I. , Biczó G. , Cser L. , Csiszár I. , Darvas I. , Gulácsy Sára , Györösi P. , Harza T. , Holderith J. , Huang Ha Szol , Huszár M. , Ire T. , Ivanyos A. , Kálmán Gy. , Kása I. , Katz T. , Kim Kvang Jan , Kiss P. , Komáromy B. , Krakóczki F. , Krem A. , Legéndy K. , Makkai M. , Mecseki A. , Mestyán Anna , No Mjang Gi , Pasitka B. , Pátkai Gy. , Pintér L. , Quittner P. , Rázga T. , Rédl J. , Rétey Piroska , Riba D. , Szabados J. , Szabó E. , Szeidl B. , Szentai E. , Szentkirályi Klára , Szlanka I. , Szy Leona , Turóczy B. , Vásárhelyi B. , Vértes P. , Zs. Nagy I. , Zsombok Z.
Füzet:	1955/március, 87 - 90. oldal		PDF \| MathML
Témakör(ök):	Párhuzamos szelők tétele, Háromszögek szerkesztése, Feladat
Hivatkozás(ok):	Feladatok: 1954/október: 635. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás: Képzeljük a feladatot megoldottnak. A betűzést az 1. ábra mutatja.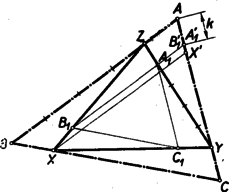

1. ábra

Osszuk fel az

X Y Z ▵

oldalait az

A_{1}

B_{1}

C_{1}

pontokkal

\frac{A_{1} Y}{A_{1} Z} = \frac{B_{1} Z}{B_{1} X} = \frac{C_{1} X}{C_{1} Y} = \frac{1}{λ}

arányban. Be fogjuk bizonyítani, hogy az

A_{1} B_{1} C_{1} ▵

oldalai rendre párhuzamosak az

A B C ▵

oldalaival.
Húzzuk az

X

A_{1}

és

B_{1}

pontokon keresztül párhuzamosokat az

A B

oldallal, és messék ezek a párhuzamosok az

A C

oldalt rendre az

X'

A'_{1}

B'_{1}

pontokban.

\begin{matrix} \frac{X' C}{X' A} = \frac{X C}{X B} = \frac{1}{λ} = \frac{Y A}{Y C} . \end{matrix}

Ebből következik, hogy

\begin{matrix} A X' = Y C = λ \cdot Y A . \end{matrix}

(1)

Jelöljük az egyszerűség kedvéért az

A'_{1} A

távolságot

k

-val. (

A A'_{1} = - k

\begin{matrix} \frac{A'_{1} Y}{k} = \frac{A_{1} Y}{A_{1} Z} = \frac{1}{λ}, amiből A'_{1} Y = \frac{k}{λ} \end{matrix}

(2)

(1) és (2) figyelembevételével

\begin{matrix} \frac{A'_{1} A}{A'_{1} X'} = \frac{k}{A X' - A A'_{1}} = \frac{k}{A X' + k} = \frac{k}{λ \cdot Y A + k} = \frac{k}{λ (Y A'_{1} + A'_{1} A) + k} = \\ = \frac{k}{λ (- \frac{k}{λ} + k) + k} = \frac{k}{- k + λ k + k} = \frac{1}{λ} . \end{matrix}

De ugyanilyen arányban osztja a

B'_{1}

pont is a

A X'

távolságot. Ugyanis

\begin{matrix} \frac{B'_{1} A}{B'_{1} X'} = \frac{B_{1} Z}{B_{1} X} = \frac{1}{λ} . \end{matrix}

Tehát

\begin{matrix} A'_{1} \equiv B'_{1}, \end{matrix}

vagyis tényleg

\begin{matrix} A_{1} B_{1} ∥ A B . \end{matrix}

Eszerint a szerkesztés menete: Megszerkesztjük az

X Y Z ▵

oldalain az

A_{1}

B_{1}

C_{1}

pontokat úgy, hogy

\begin{matrix} \frac{A_{1} Y}{A_{1} Z} = \frac{B_{1} Z}{B_{1} X} = \frac{C_{1} X}{C_{1} Y} = \frac{1}{λ}, és a Z, X, Y \end{matrix}

pontokon át rendre párhuzamosokat húzunk az

A_{1} B_{1} C_{1} ▵

oldalaival.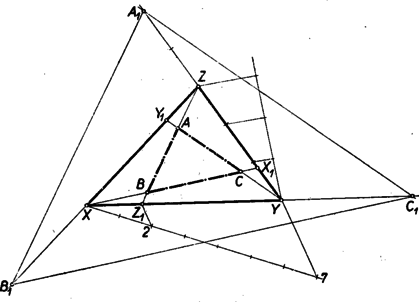

\begin{matrix} λ = - \frac{1}{4} esetén \frac{1}{λ} = - 4 (1. ábra) \\ λ = \frac{2}{5} esetén \frac{1}{λ} = \frac{5}{2} (2. ábra) . \end{matrix}

2. ábra

Speciális esetek:

λ = 0

esetén

A_{1} \equiv Z

B_{1} \equiv X

C_{1} \equiv Y

, és így

A \equiv Z

B \equiv X

C \equiv Y

λ = - 1

esetén

\frac{1}{λ} = - 1

, és így az

A_{1}

B_{1}

C_{1}

pontok az

X Y Z ▵

oldalainak felezőpontjai, tehát az

A_{1} B_{1} C_{1} ▵

oldalai az

X Y Z ▵

középvonalai, vagyis

A B ∥ X Y

B C ∥ Y Z

C A ∥ Z X

. (Triviális eset, midőn

X

Y

Z

A B C ▵

oldalainak felezőpontjai.)

λ = 1

esetén

\frac{1}{λ}

is egyenlő az egységgel, és szerkesztésünk csődöt mond, mert az

A_{1}

B_{1}

C_{1}

pontok nincsenek a végesben. Ez esetben tulajdonképpen a sík bármely

P

pontja tekinthető egy ponttá fajuló megoldásnak (

A \equiv B \equiv C \equiv P

II. megoldás: Képzeljük a feladatot megoldottnak. A betűzést a 3. ábra mutatja.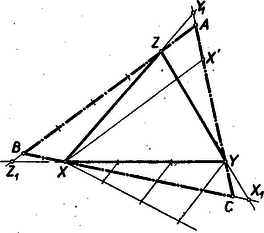

3. ábra

Jelöljük az

A B

és

X Y

egyenesek metszéspontját

Z_{1}

-gyel. Az

X

ponton keresztül

A B

-vel párhuzamos egyenes messe az

A C

oldalt

X'

-ben (3. ábra).

\begin{matrix} \frac{B C}{B X} = \frac{B X + X C}{B X} = 1 - \frac{X C}{X B} = \\ = 1 - \frac{1}{λ} = \frac{λ - 1}{λ} = \frac{A C}{A X'}, \end{matrix}

amiből

\begin{matrix} A X' = \frac{λ \cdot A C}{λ - 1} = - \frac{λ \cdot A C}{1 - λ} \end{matrix}

(1)

(Végesben fekvő osztópont esetén

λ \neq 1

, vagyis

λ - 1 \neq 0

\begin{matrix} \frac{C A}{C Y} = \frac{C Y + Y A}{C Y} = 1 - \frac{Y A}{Y C} = 1 - \frac{1}{λ} = \frac{λ - 1}{λ}, \end{matrix}

ahonnan

\begin{matrix} C Y = \frac{λ \cdot C A}{λ - 1} = \frac{λ \cdot A C}{1 - λ} . \end{matrix}

(2)

(2) felhasználásával

\begin{matrix} A Y = A C + C Y = A C + \frac{λ \cdot A C}{1 - λ} = \frac{A C - λ \cdot A C + λ \cdot A C}{1 - λ} = \frac{A C}{1 - λ} . \end{matrix}

(3)

(1) és (3) figyelembevételével

\begin{matrix} \frac{Z_{1} X}{Z_{1} Y} = \frac{A X'}{A Y} = \frac{- \frac{λ \cdot A C}{1 - λ}}{\frac{A C}{1 - λ}} = - λ . \end{matrix}

Tehát a szerkesztés menete: Megszerkesztjük

X Y Z ▵

oldalain rendre a

Z_{1}

X_{1}

Y_{1}

pontokat úgy, hogy

\frac{Z_{1} X}{Z_{1} Y} = \frac{X_{1} Y}{X_{1} Z} = \frac{Y_{1} Z}{Y_{1} X} = - λ

; a

Z Z_{1}

X X_{1}

Y Y_{1}

egyenesek rendre az

A B C ▵

oldalainak hordozói.

λ = - \frac{1}{4}

esetén

- λ = \frac{1}{4}

(3. ábra),

λ = \frac{2}{5}

esetén

- λ = - \frac{2}{5}

(2. ábra).

Speciális esetek:

λ = 0

esetén

- λ

is egyenlő nullával, vagyis

Z_{1} \equiv X

X_{1} \equiv Y

és

Y_{1} \equiv Z

és így

A \equiv Z

B \equiv X

C \equiv Y

.
Ha

λ = - 1

, akkor

- λ = 1

, vagyis

Z Z_{1} ∥ X Y

X X_{1} ∥ Y Z

Y Y_{1} ∥ Z X

. (Triviális eset, midőn az

X

Y

Z

pontok felezik az

A B C ▵

oldalait.)

λ = 1

esetén

- λ = - 1

, vagyis az

X X_{1}

Y Y_{1}

Z Z_{1}

egyenesek az

X Y Z ▵

súlyvonalai, és így az

A B C

‐ mint határeset ‐ az

X Y Z ▵

súlypontjává fajul. (

A \equiv B \equiv C \equiv S

. ‐ Lásd I. megoldást.)

Megjegyzés: Egy megoldó sem dolgozott irányított távolságokkal, és senki sem adott általános érvényű, egységesen az osztóviszonnyal kifejezett megoldást.