Kezdőlap


Feladat:	634. matematika feladat	Korcsoport: 18-	Nehézségi fok: átlagos
Megoldó(k):	Frivaldszky Sándor , Katz Tibor
Füzet:	1955/március, 86 - 87. oldal		PDF \| MathML
Témakör(ök):	Terület, felszín, Szélsőérték-feladatok differenciálszámítás nélkül, Feladat
Hivatkozás(ok):	Feladatok: 1954/október: 634. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás: Legyen $A P = x$ a tetraéder éle akkor a tetraéder felszíne $4 \cdot \frac{x^{2}}{4} \sqrt[]{3} = x^{2} \sqrt[]{3}$ , a hexaéder felszíne $6 {(a - x)}^{2}$ .
Tehát az

\begin{matrix} y = x^{2} \sqrt[]{3} + 6 {(a - x)}^{2} = (6 + \sqrt[]{3}) x^{2} - 12 a x + 6 a^{2} \end{matrix}

másodfokú függvény minimumát keressük. (Minimum van, mert

x^{2}

együtthatója pozitív.)
Ismeretes, hogy az

y = a x^{2} + b x + c

másodfokú függvénynek szélső érteke az

x_{0} = - \frac{b}{2 a}

helyen van. Jelen esetre alkalmazva

\begin{matrix} x_{0} = \frac{12 a}{12 + 2 \sqrt[]{3}} = \frac{6 a}{6 + \sqrt[]{3}} . \end{matrix}

Tehát

\begin{matrix} A P = \frac{6 a}{6 + \sqrt[]{3}}, \\ B P = a - x = a - \frac{6 a}{6 + \sqrt[]{3}} = \frac{a \sqrt[]{3}}{6 + \sqrt[]{3}} \end{matrix}

és így

\begin{matrix} \frac{A P}{P B} = \frac{6}{\sqrt[]{3}} = \frac{2 \sqrt[]{3}}{1} = \frac{\sqrt[]{12}}{1}, \end{matrix}

A B

távolságnak a

\sqrt[]{3 \cdot 4} : 1

arányban való osztását az 1. ábra mutatja.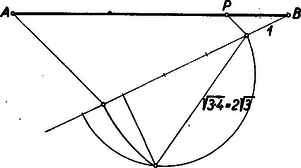

1. ábra

\sqrt[]{12}

-t, mint 3 és 4 közötti mértani középarányost szerkesztettük meg a derékszögű háromszög ismeretes arányossági tétele alapján.

Frivaldszky Sándor (Bp. II., Rákóczi g. II. o. t.)

II. megoldás: Minden számítás nélkül is megszerkeszthetjük a minimális felszínt és ezzel a

P

pontot.
A felszín negyedrésze éppen egy tetraéderlap és

1, 5

kockalap felszínének összege. Vizsgáljuk meg, miként változik e két terület összege, ha a

P

pont végigfut az

A B

szakaszon.

2. ábra

P

pont tetszőleges helyzetét jelöljük

P'

-vel (2. ábra); a hozzátartozó tetraéderlap az

A C P'

szabályos háromszög, a

P'

-höz tartozó

1, 5

kockalap olyan téglalappal szemléltethető, melynek egyik oldala

B P'

, a másik

B E = P' D = 1, 5 P' B

. Mindkét idomot alakítsuk át derékszögű háromszöggé úgy, hogy a közös befogójuk a

P'

-ben

A B

-re emelt merőleges legyen, másik befogójuk

P' A

, ill.

P' B

. A tetraéderlap területe az

A P' C'

háromszöggel helyettesíthető, a kockalap területe pedig a

B P' H'

háromszöggel (

P' H' = 3 P' B

). Az átfogók egyenese független a

P'

pont helyzetétől, mert az

A

-ból kiinduló átfogó

A B

-vel bezárt szögére nézve, fennáll, hogy

tg α = \frac{\sqrt[]{3}}{2}

, a

B

-ből kiinduló átfogónak

A B

-vel bezárt szögére pedig

tg β = 3

. E két rögzített egyenes metszéspontját jelöljük

M

-mel. A

P'

pont változtatásával

C'

A M

átfogón mozog,

H'

pedig a

B M

átfogón.
A két poliéder felszínének negyedrészét az

A C' H' B

négyszög szemlélteti. E négyszög az

A M B

állandó háromszögből és a srafozott

M C' H'

változó háromszögből tevődik össze.

P'

változtatásával csak ez utóbbi háromszög területe változik; legkisebb akkor, ha éppen 0, azaz

C'

és

H'

egybeesik

M

-mel.

M

pont és a hozzátartozó

P

szerkesztése az ábrából leolvasható.
Megjegyzés: Most a megszerkesztett

A P

távolság hosszát számíthatjuk ki utólag a szerkesztés alapján az

α

és

β

szögek segítségével. Ugyanis

M P = x tg α = (a - x) tg β

, vagyis

x \frac{\sqrt[]{3}}{2} = (a - x) 3

, amiből

x = \frac{6 a}{6 + \sqrt[]{3}}

Katz Tibor (Hajdúnánás, Körösi Csoma g. III. o. t.)