Kezdőlap


Feladat:	632. matematika feladat	Korcsoport: 18-	Nehézségi fok: átlagos
Megoldó(k):	Benkő Bálint , Gerencsér Piroska , Kovács István , Rázga Tamás
Füzet:	1955/március, 82 - 84. oldal		PDF \| MathML
Témakör(ök):	Szögfüggvények, síkgeometriai számítások, Feladat
Hivatkozás(ok):	Feladatok: 1954/október: 632. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás: Az ismert

\begin{matrix} tg \frac{α}{2} = \sqrt[]{\frac{1 - cos α}{1 + cos α}} \end{matrix}

képlet felhasználásával

\begin{matrix} {tg}^{2} \frac{α}{2} = \frac{1}{4} = \frac{1 - cos α}{1 + cos α} = \frac{1 - \frac{b}{c}}{1 + \frac{b}{c}} = \frac{c - b}{c + b} = \frac{c - b}{14}, \end{matrix}

amiből

\begin{matrix} c - b = \frac{14}{4} = \frac{7}{2}, \end{matrix}

(1)

a feladat szerint

\begin{matrix} c + b = 14. \end{matrix}

(2)

(1) és (2)-ből

\begin{matrix} c = \frac{35}{4} = 8,75 cm és b = \frac{21}{4} = 5,25 cm, \end{matrix}

és így

\begin{matrix} a = \sqrt[]{\frac{35^{2} - 21^{2}}{16}} = \sqrt[]{\frac{56 \cdot 14}{16}} = \sqrt[]{\frac{16 \cdot 49}{16}} = 7 cm . \end{matrix}

Gerencsér Piroska (Bp., VIII., Zrínyi Ilona lg. IV. o. t.)

II. megoldás: Felhasználhatjuk a

\begin{matrix} tg α = \frac{2 tg \frac{α}{2}}{1 - {tg}^{2} \frac{α}{2}} \end{matrix}

képletet is.

\begin{matrix} tg α = \frac{a}{b} = \frac{2 \cdot \frac{1}{2}}{1 - \frac{1}{4}} = \frac{4}{3} . \end{matrix}

Tehát egy alkalmas

λ

arányossági tényezővel a háromszög oldalai ilyen alakúak:

\begin{matrix} a = 4 λ, b = 3 λ, és c = \sqrt[]{a^{2} + b^{2}} = \sqrt[]{16 λ^{2} + 9 λ^{2}} = 5 λ . \end{matrix}

A feladat szerint

\begin{matrix} b + c = 8 λ = 14, \end{matrix}

amibő

\begin{matrix} λ = \frac{7}{4} . \end{matrix}

Kovács István (Bp., VIII., Piarista g. IV. o. t.)

III. megoldás: Trigonometriai képletek nélkül is célhoz érhetünk. Az

α

szög felezője az

a

oldalt

x

és

y

részekre osztja. (Lásd ábrát.)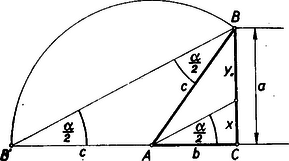

Ismeretes tétel alapján

\begin{matrix} \frac{x}{y} = \frac{b}{c} . \end{matrix}

(1)

Mivel a feladat szerint

tg \frac{α}{2} = \frac{1}{2} = \frac{x}{b}

, azért

x = \frac{b}{2}

, és így (1) alapján

\begin{matrix} y = \frac{c}{2} . \end{matrix}

Tehát

\begin{matrix} a = x + y = \frac{b + c}{2} = \frac{14}{2} = 7. \end{matrix}

Pythagoras tétele szerint

\begin{matrix} 7^{2} + b^{2} = {(14 - b)}^{2} = 196 - 28 b + b^{2}, \end{matrix}

ahonnan

\begin{matrix} 28 b = 147, és így b = \frac{147}{28} = \frac{21}{4} stb . \end{matrix}

Benkő Bálint (Sárospatak, Rákóczi g. III. o. t.)

IV. megoldás: Még a szögfelező‐tételt is nélkülözhetjük. Forgassuk

A B = c

átfogót

A

körül az

A C = b

oldal meghosszabbításába:

A B' = c

. (Lásd ábrát.) Akkor nyilván

\begin{matrix} B' C = b + c = 14, \end{matrix}

és a

\begin{matrix} B B' C ∢ = \frac{α}{2} . \end{matrix}

Tehát a

B B' C

derékszögű háromszögből

\begin{matrix} a = (b + c) tg \frac{α}{2} = 14 \cdot \frac{1}{2} = 7 \end{matrix}

stb., mint a III. megoldásban.

Rázga Tamás (Bp. II., Rákóczi g. III. o. t.)