Kezdőlap


Feladat:	626. matematika feladat	Korcsoport: 18-	Nehézségi fok: átlagos
Megoldó(k):	Daróczy Zoltán , Gerencsér Piroska
Füzet:	1955/március, 75 - 77. oldal		PDF \| MathML
Témakör(ök):	Egyenesek egyenlete, Ellipszis egyenlete, Feladat
Hivatkozás(ok):	Feladatok: 1954/szeptember: 626. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás: Az állítást elegendő a félátmérőkre bizonyítani, mert ha ezekre igaz, nyilván igaz kétszeresükre is.
Abban a speciális esetben, amikor a két, egymásra merőleges átmérő éppen a nagy- és a kistengely, a reciprok értékek négyzetösszege:

\begin{matrix} \frac{1}{a^{2}} + \frac{1}{b^{2}} = \frac{b^{2} + a^{2}}{a^{2} b^{2}} . \end{matrix}

Így tehát, ha a tétel igaz, az állandó szükségképpen

\begin{matrix} \frac{a^{2} + b^{2}}{a^{2} b^{2}} \end{matrix}

Vegyük fel a koordináta‐rendszer kezdőpontját a nagy- és kistengely metszéspontjában, az ellipszis tengelyei pedig illeszkedjenek a koordináta-rendszer tengelyeihez. Ez esetben, mint ismeretes, az

a

b

féltengelyű ellipszis egyenlete:

\begin{matrix} \frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1. \end{matrix}

Legyen az egyik félátmérő egyenesének egyenlete

y = m x

, akkor a reá merőleges másik félátmérő egyenesének egyenlete

y = - \frac{1}{m} x

. Behelyettesítéssel kiszámítva az ellipszis és a két átmérő egyenes egy‐egy metszéspontjának (az átmérő egy-egy végpontjának) koordinátáit:

\begin{matrix} x_{1}^{2} & = \frac{a^{2} b^{2}}{b^{2} + a^{2} m^{2}}, y_{1}^{2} = \frac{a^{2} b^{2} m^{2}}{b^{2} + a^{2} m^{2}}, \\ x_{2}^{2} & = \frac{a^{2} b^{2} m^{2}}{a^{2} + b^{2} m^{2}}, y_{2}^{2} = \frac{a^{2} b^{2}}{a^{2} + b^{2} m^{2}}, \end{matrix}

akkor a két félátmérő hosszának négyzete

\begin{matrix} e^{2} & = x_{1}^{2} + y_{1}^{2} = \frac{a^{2} b^{2} (m^{2} + 1)}{a^{2} m^{2} + b^{2}}, \\ f^{2} & = x_{2}^{2} + y_{2}^{2} = \frac{a^{2} b^{2} (m^{2} + 1)}{a^{2} + b^{2} m^{2}} . \end{matrix}

Ebből pedig a reciprokok négyzetösszege :

\begin{matrix} \frac{1}{e^{2}} + \frac{1}{f^{2}} = \frac{(a^{2} + b^{2}) + (a^{2} + b^{2}) m^{2}}{a^{2} b^{2} (m^{2} + 1)} = \frac{(a^{2} + b^{2}) (1 + m^{2})}{a^{2} b^{2} (m^{2} + 1)} = \frac{a^{2} + b^{2}}{a^{2} b^{2}} \end{matrix}

ami valóban független az

m

-től, vagyis minden egymásra merőleges átmérőpárra ugyanaz.

Gerencsér Piroska (Bp. VIII., Zrínyi Ilona lg. IV. o. t.)

II. megoldás: A betűzést az ábra mutatja. Fejezzük ki a félátmérők végpontjainak koordinátáit a félátmérők hosszával és a félátmérőknek az

x

tengellyel bezárt szögével.

A

P

pont koordinátái:

\begin{matrix} x_{1} = e cos α, y_{1} = e sin α, \end{matrix}

Q

pont koordinátái:

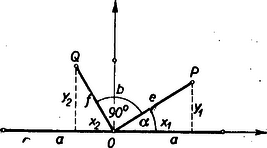\begin{matrix} x_{2} & = f cos (α + 90^{\circ}) = f sin α, \\ y_{2} & = f sin (α + 90^{\circ}) = f cos α . \end{matrix}

Mivel

P

és

Q

az ellipszis pontjai, ezért e koordináták kielégítik annak egyenletét:

\begin{matrix} \frac{e^{2} cos^{2} α}{a^{2}} + \frac{e^{2} sin^{2} α}{b^{2}} = 1, és \frac{f^{2} sin^{2} α}{a^{2}} + \frac{f^{2} cos^{2} α}{b^{2}} = 1. \end{matrix}

Ebből

\begin{matrix} \frac{1}{e^{2}} = \frac{cos^{2} α}{a^{2}} + \frac{sin^{2} α}{b^{2}}, és \frac{1}{f^{2}} = \frac{sin^{2} α}{a^{2}} + \frac{cos^{2} α}{b^{2}} . \end{matrix}

E két egyenlet összege

\begin{matrix} \frac{1}{e^{2}} + \frac{1}{f^{2}} = \frac{1}{a^{2}} (cos^{2} α + sin^{2} α) + \frac{1}{b^{2}} (sin^{2} α + cos^{2} α) = \frac{1}{a^{2}} + \frac{1}{b^{2}}, \end{matrix}

ami valóban állandó.

Daróczy Zoltán (Debrecen, Ref. g. III. o. t.)