Kezdőlap


Feladat:	625. matematika feladat	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Biczó Géza , Szabados József , Weiling Károly
Füzet:	1955/március, 72 - 75. oldal		PDF \| MathML
Témakör(ök):	Síkgeometriai számítások trigonometria nélkül háromszögekben, Szögfüggvények, síkgeometriai számítások, Feladat
Hivatkozás(ok):	Feladatok: 1954/szeptember: 625. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás: A betűzést az 1. ábra mutatja.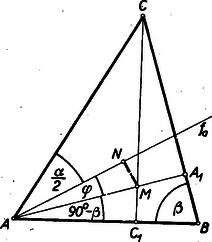

1. ábra

Induljunk ki a

\begin{matrix} 2 \cdot M N = b - c \end{matrix}

(1)

egyenletből. Ezt úgy kell átalakítanunk, hogy kiszámíthassuk belőle

α

-t, ami csak úgy sikerülhet, ha az átalakított egyenletből

α

kivételével a háromszög minden más alkotórésze kiküszöbölődik és

α

-ra egy tiszta goniometriai egyenlet marad. Célszerű lesz tehát arra törekedni, hogy az egyenlet mindkét oldalán egyetlen (mégpedig ugyanazon) hosszúság szerepeljen, ezenkívül pedig csak a háromszög szögei (ill. a szögek függvényei).
A baloldal átalakítása: Az

A M N

derékszögű háromszögből

M N = A M sin φ

, ahol

\begin{matrix} φ = \frac{α}{2} - (90^{\circ} - β) = \frac{α + 2 β - 180^{\circ}}{2} = \frac{α + 2 β - (α + β + γ)}{2} = \frac{β - γ}{2} . \end{matrix}

A M C_{1}

derékszögű háromszögből

\begin{matrix} A M = \frac{A C_{1}}{sin β}, \end{matrix}

A C C_{1}

derékszögű háromszögből

\begin{matrix} A C_{1} = b cos α . \end{matrix}

Ezeknek az értékeknek visszahelyettesítése után (1) baloldala így alakul át

\begin{matrix} 2 \cdot M N = \frac{b cos α}{sin β} \cdot 2 sin \frac{β - γ}{2} . \end{matrix}

A jobboldalt is átalakítjuk úgy, hogy csak a szögek és

b

szerepeljen benne. A sinus-tétel szerint

c = \frac{b sin γ}{sin β}

, tehát

\begin{matrix} b - c = b - \frac{b sin γ}{sin β} = b \frac{sin β - sin γ}{sin β} . \end{matrix}

Felírva az átalakított (1) egyenletet és egyszerűsítve

\frac{b}{sin β}

-val

(b \neq 0

sin β \neq 0

)

\begin{matrix} cos α \cdot 2 sin \frac{β - γ}{2} = sin β - sin γ . \end{matrix}

A baloldalt szorozzuk

cos \frac{β + γ}{2}

-vel, a jobboldalt pedig a vele egyenlő

sin \frac{α}{2}

-vel

\begin{matrix} cos α (2 cos \frac{β + γ}{2} sin \frac{β - γ}{2}) = (sin β - sin γ) sin \frac{α}{2} . \end{matrix}

Mint ismeretes, a baloldali zárójelbe foglalt szorzat azonosan egyenlő (

sin β - sin γ

)-val. Ha az értéke 0, akkor

β = γ

, tehát a háromszög egyenlő szárú, melyre (1) fennáll, de triviális. Ha

sin β - sin γ \neq 0

, akkor (

sin β - sin γ

)-val egyszerűsítve a

\begin{matrix} cos α = sin \frac{α}{2} \end{matrix}

egyenletre jutunk.

cos α

helyébe

1 - 2 sin^{2} \frac{α}{2}

-t írva és rendezve

\begin{matrix} 2 sin^{2} \frac{α}{2} + sin \frac{α}{2} - 1 = 0, \end{matrix}

amiből

\begin{matrix} sin \frac{α}{2} = \frac{- 1 \pm \sqrt[]{1 + 8}}{4} . \end{matrix}

A feladat szerint csak a pozitív gyöknek van értelme, tehát

sin \frac{α}{2} = \frac{1}{2}

, ahonnan

(\frac{α}{2} < 90^{\circ} miatt)

csak

α = 60^{\circ}

felel meg a feladat követelményeinek.

Biczó Géza (Bp. II. Rákóczi g. IV. o. t.)

2. ábra

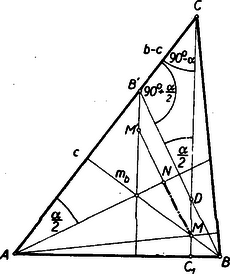II. megoldás: A betűzést a 2. ábra mutatja. Meg fogjuk kísérelni a

\begin{matrix} 2 \cdot M N = b - c \end{matrix}

(1)

összefüggés felhasználásával

α

-t szögfüggvények nélkül, tisztán a szögek közötti összefüggések alapján, meghatározni. E célból az ábrát kiegészítjük.
Tükrözzük

B

-t és

M

-et

f_{a}

-ra, így nyerjük az

A B B'

egyenlőszárú háromszöget és az

M'

pontot.

A B' = c

és

B' C = b - c

. Az egyenlőszárú háromszög

B

-ből kiinduló magassága és az eredeti háromszög

m_{b}

magassága azonos, az egyenlőszárú háromszög

B'

-ből kiinduló magassága tehát

m_{b}

-nek

f_{a}

-ra vonatkozó tükörképe és így átmegy az

M'

ponton.
Az eredeti háromszög

m_{c}

magasságvonala messe

B B'

-t a

D

pontban. A

D B' M' M

idom paralelogramma (mert a szemközti oldalai párhuzamosak), ezért

M M' = D B'

.
A

B' D C

háromszög

B

-nél fekvő szöge

90^{\circ} + \frac{α}{2}

(mert külső szöge egy olyan derékszögű háromszögnek, melynek másik hegyesszöge

\frac{α}{2}

), a

C

-nél fekvő szöge az

A C_{1} C

derékszögű háromszögből

90^{\circ} - α

, a

D

-nél fekvő szöge pedig, mint merőleges szárú szög,

\frac{α}{2} (90^{\circ} + \frac{α}{2} + 90^{\circ} - α + \frac{α}{2} = 180^{\circ})

(1) akkor teljesül, ha

2 M N = B' D = B' C

, vagyis

C B' D ▵

egyenlőszárú s így

\begin{matrix} \frac{α}{2} = 90^{\circ} - α, amiből α = 60^{\circ} . \end{matrix}

Szabados József (Bp. III., Árpád g. III. o. t.)

Általánosítások:

1. Ha tetszőleges, rögzített

α

szög szárán a

C

pont mozog, akkor változik a

B' C = b - c

távolság és vele együtt változik az

M

és

N

pont is, de állandóan igaz marad, hogy

B' D # M M' = 2 M N

és a

B' D C △

csak nagyságra változik, de alakra nem (2. ábra). Ez utóbbi változó háromszögeknek (csak

α

-tól függő) szögei tehát állandóak, és így a

B' C

és

B' D

oldalak aránya

\begin{matrix} \frac{b - c}{2 M N} = k, \end{matrix}

ahol

k

konstans, amíg

α

is az.
A sinus‐tétel alapján

\begin{matrix} \frac{b - c}{2 M N} = \frac{sin \frac{α}{2}}{sin (90^{\circ} - α)}, vagyis \\ \frac{b - c}{M N} = \frac{2 sin \frac{α}{2}}{cos α} = k . \end{matrix}

Ezzel általában bebizonyítottuk, hogy minden

α

szöghöz tartozik egy állandó

k = \frac{b - c}{M N}

arányszám.

(Jelen példában

k = 2

, amiből következik, hogy

\frac{sin \frac{α}{2}}{cos α} = 1

, vagyis

α = 60^{\circ}

)

Weiling Károly (Diósgyőr, Kilián Gy. g. IV. o. t.)

2. Feladatunk tulajdonképpeni általánosítása azonban a fenti általánosításnak megfordítása: adott pozitív

k

számhoz meghatározni az

α

szöget úgy, hogy

\frac{b - c}{M N} = k

. Tehát tulajdonképpen a

\begin{matrix} sin \frac{α}{2} = \frac{k}{2} cos α \end{matrix}

goniometriai egyenlet megoldásáról van szó. Grafikus ábrázolással könnyen meggyőződhetünk, hogy

α

-ra mindig van egy és csakis egy megoldás a

(0, \frac{π}{2})

intervallumban, de az I. megoldásban mutatott út

(cos α = 1 - 2 sin^{2} \frac{α}{2})

itt is követhető, és a

sin \frac{α}{2}

-re nyert másodfokú egyenletnek pozitív gyöke:

\begin{matrix} sin \frac{α}{2} = \frac{\sqrt[]{1 + 2 k^{2}} - 1}{2 k} . \end{matrix}

Könnyű megmutatni, hogy ha

k > 0

, akkor

\begin{matrix} 0 < \frac{\sqrt[]{2 k^{2} + 1} - 1}{2 k} < \frac{\sqrt[]{2}}{2}, és így 0 < \frac{α}{2} < \frac{π}{4} . \end{matrix}