Kezdőlap


Feladat:	624. matematika feladat	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Bártfai Pál , Darvas Imre , Holderith József , Jeney Mária , Tolnai Tibor
Füzet:	1955/február, 56 - 58. oldal		PDF \| MathML
Témakör(ök):	Párhuzamos szelőszakaszok tétele, Szinusztétel alkalmazása, Koszinusztétel alkalmazása, Szabályos sokszögek geometriája, Feladat
Hivatkozás(ok):	Feladatok: 1954/szeptember: 624. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás: Bontsuk fel a szabályos hétszöget egy csúcsból kiinduló $4$ átlóval $5$ háromszögre (1. ábra), akkor az átlók a szabályos hétszög szögét $5$ egyenlő részre osztják.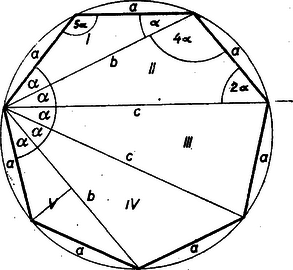

1. ábra

Egy ilyen részt

α

-val jelölve

\begin{matrix} α = \frac{1}{5} \cdot \frac{5 \cdot 180^{\circ}}{7} = \frac{180^{\circ}}{7}, vagyis 7 α = 180^{\circ}, \end{matrix}

amiből következik, hogy

\begin{matrix} sin 2 α = sin 5 α \end{matrix}

(1)

és

\begin{matrix} sin 3 α = sin 4 α . \end{matrix}

(2)

A I és II háromszögekben a szögek nagyságát az 1. ábrán jelöltük. Alkalmazzuk e két háromszögre a sinus-tételt:

\begin{matrix} \frac{a}{b} = \frac{sin α}{sin 5 α} és \frac{a}{c} = \frac{sin α}{sin 4 α} . \end{matrix}

E két egyenletet összeadva és

a

-val osztva

\begin{matrix} \frac{1}{b} + \frac{1}{c} = \frac{1}{a} (\frac{sin α}{sin 5 α} + \frac{sin α}{sin 4 α}) . \end{matrix}

(1) és (2) figyelembevételével a zárójeles kifejezés

\begin{matrix} \frac{sin α (sin 4 α + sin 2 α)}{sin 2 α sin 4 α} = \frac{sin α \cdot 2 sin 3 α cos α}{sin 2 α sin 3 α} = 1 \end{matrix}

és ezzel tételünket bebizonyítottuk.

Bártfai Pál (Bp. I., Petőfi g. IV. o. t.)

II. megoldás: Az 1. ábrán az V egyenlőszárú háromszögben meghúzva a

b

alaphoz tartozó magasságot, leolvashatjuk, hogy

\begin{matrix} cos α = \frac{b}{2 α} . \end{matrix}

(1)

A IV és III háromszögek

a

oldalára alkalmazva a cosinus-tételt,

cos α

helyett az (1) alatti értéket írva

\begin{matrix} a^{2} = b^{2} + c^{2} - 2 b c \frac{b}{2 a} = b^{2} + c^{2} - \frac{b^{2} c}{a}, \end{matrix}

(2)

illetőleg

\begin{matrix} a^{2} = c^{2} + c^{2} - 2 c^{2} \frac{b}{2 a} = 2 c^{2} - \frac{b c^{2}}{a} . \end{matrix}

(3)

Mivel (2) és (3)-ban a baloldalak egyenlők, azért a jobboldalak is azok, vagyis (

a

-val szorozva)

\begin{matrix} a b^{2} + a c^{2} - b^{2} c = 2 a c^{2} - b c^{2} . \end{matrix}

(4)

Rendezve

\begin{matrix} b c^{2} - b^{2} c = a c^{2} - a b^{2}, \end{matrix}

vagyis

\begin{matrix} b c (c - b) = a (c^{2} - b^{2}) . \end{matrix}

Midkét oldalt

a b c (a - b)

-vel osztva (

c \neq b

)

\begin{matrix} \frac{1}{a} = \frac{c + b}{b c} = \frac{1}{b} + \frac{1}{c} . \end{matrix}

Tolnai Tibor (Szombathely, Nagy Lajos g. IV. o. t.)

III. megoldás: Az

A B C D E F G

hétszögben jelöljük az

A D

és

C G

átlók metszéspontját

M

-mel (2. ábr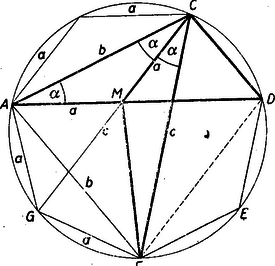a).

2. ábra

Mivel

A D | | B C

és

C G | | A B

, ezért

A B C M

rombusz, és így

M C = a

.
Az

A C D ▵

területe

\begin{matrix} t_{A C D} = t_{A C M} + t_{M C D} . \end{matrix}

Mivel

D F | | C G

, azért

\begin{matrix} t_{M C D} = t_{M C F}, \end{matrix}

és így

\begin{matrix} t_{A C D} = t_{A C M} + t_{M C F}, \end{matrix}

vagyis

\begin{matrix} \frac{b c sin α}{2} = \frac{a b sin α}{2} + \frac{a c sin α}{2} . \end{matrix}

Mindkét oldalt

\frac{2}{a b c sin α}

-val szorozva

\begin{matrix} \frac{1}{a} = \frac{1}{c} + \frac{1}{b} . \end{matrix}

Jeney Mária (Debrecen, Svetits lg. III. o. t.)

IV. megoldás: Még gyorsabban célhoz vezet a ‐ trigonometriát nem is igénylő ‐ Ptolemaios-tétel. Mint ismeretes, e tétel szerint a húrnégyszögben az átlók szorzata egyenlő a szemközti oldalpárok szorzatának összegével.
Az

A C F G

(2. ábra) húrnégyszögre alkalmazva

\begin{matrix} b c = a b + a c, \end{matrix}

vagyis (

a b c

-vel osztva)

\begin{matrix} \frac{1}{a} = \frac{1}{c} + \frac{1}{b} . \end{matrix}

Holderith József (Bp. XIV., Vegyip. techn. IV. o t.)

V. megoldás: Még egyszerűbb eszközök: metszetek arányossága is elegendő tételünk bizonyításához.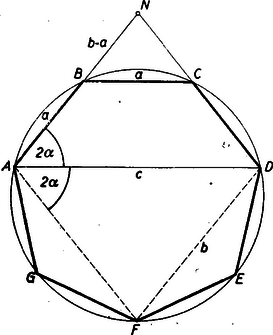

3. ábra

Ha az

A B

és

C D

oldalak metszéspontját

N

-nel jelöljük (3. ábra), akkor

A N D F

nyilván rombusz és így

N A = D F = b

. Mivel

B C | | A D

, ezért

\begin{matrix} N B : B C = N A : A D, \end{matrix}

vagyis

\begin{matrix} (b - a) : a = b : c, \end{matrix}

amiből

\begin{matrix} b c - a c = a b, azaz b c = a c + a b . \end{matrix}

Darvas Imre (Kaposvár, Táncsics g. IV. o. t.)