Kezdőlap


Feladat:	620. matematika feladat	Korcsoport: 18-	Nehézségi fok: nehéz
Megoldó(k):	Biczó G. , Csiszár I. , Edöcsény L. , Eördögh L. , Kálmán Gy. , Kovács László , Mecseki A. , Quittner P. , Rázga T. , Siklósi P. , Szabó E. , Tomor B. , Vigassy Gy. , Vigassy József , Zawadowski Alfréd , Zsombok Z.
Füzet:	1955/február, 51 - 54. oldal		PDF \| MathML
Témakör(ök):	Terület, felszín, Térfogat, Geometriai valószínűség, Feladat
Hivatkozás(ok):	Feladatok: 1954/május: 620. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás: Legyen a kiválasztandó három szakasz $a$ , $b$ , $c < 1$ . Minden lehetséges kiválasztás egy számhármassal jellemezhető. A $≫$ kedvező $≪$ és $≫$ lehetséges $≪$ esetek összehasonlítása céljából ezeket alkalmas módon ábrázolni fogjuk.
A számhármasokat közvetlenül ábrázolhatjuk térbeli koordinátarendszerben a tér egy-egy pontjával (lásd a II. megoldást). A síkbeli koordinátarendszer közvetlenül csak számpárok ábrázolására alkalmas. Ezért egyelőre az egyik oldalt, pl. $a$ -t állandónak tekintjük, és megvizsgáljuk, mi a valószínűsége annak, hogy rögzített $a$ mellett, változó $b$ és $c$ -vel háromszöget lehessen szerkeszteni. A rögzített $a$ -hoz tartozó $(b, c)$ számpárt a szokásos módon derékszögű koordinátarendszerben ábrázolhatjuk oly ponttal, melynek abszcisszája $b$ , ordinátája $c$ (1. ábr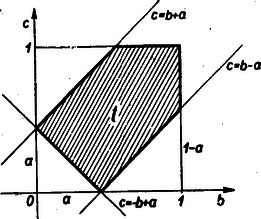a).

1. ábra

A háromszög megszerkeszthetőségének feltételei

\begin{matrix} c < b + a; & (1) \\ c > - b + a; & (2) \\ c > b - a . & (3) \end{matrix}

Az (1) feltételnek adott

a

mellett a

c = b + a

egyenes (az egyenes irányhatározója

1

, az ordináta-tengelyből lemetszett szakasz: a) alatt fekvő pontok tesznek eleget. A (2) feltételnek a

c = - b + a

egyenes fölött fekvő, a (3) feltételnek a

c = b - a

egyenes fölött fekvő pontok tesznek eleget. Mindhárom feltételt kielégítő és az egységnégyzet belsejébe eső pontok összessége alkotja a kedvező eseteket, rögzített

a

esetén. (Az 1. ábrán a srafozott

t

terület). Az összes lehetséges esetet pedig az egységnégyzet területével

(T = 1)

jellemezhetjük. Eszerint, rögzített

a

mellett, az szerkeszthetőség valószínűsége

\begin{matrix} V_{a} = \frac{t}{T} = \frac{1 - \frac{a^{2}}{2} - 2 \frac{{(1 - a)}^{2}}{2}}{1^{2}} = - \frac{3}{2} a^{2} + 2 a \end{matrix}

(4)

Ez a valószínűség csak

a

megválasztásától függ (l. alábbi

≫

Megjegyzés

≪

-t).
Tekintsük ezután

a

-t változónak és ábrázoljuk

V_{a}

-t, mint

a

függvényét. Ezen az ábrán valamely rögzített abszcisszához tartozó kedvező eseteket a

V_{a}

ordináta, ugyanezen abszcisszához tartózó lehetséges eseteket egységnyi ordináta szakasz ábrázolja, így az

a

változtatásával létrejövő összes kedvező esetek a görbe alatti

t

területtel, míg az összes lehetséges esetet az egységnégyzet területével

(T = 1)

jellemezhetjük.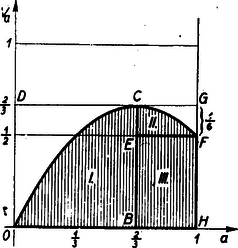

2. ábra

(4)-ből leolvashatjuk, hogy a görbe képe parabola, melynek ‐ mint ismeretes ‐ maximuma van az

a = (- 2) : (- 3) = \frac{2}{3}

helyen, ahol

V_{a}

maximális értéke

\frac{2}{3}

(2. ábra). A görbe alatti terület I része az

O B C D

négyzet

\frac{2}{3}

része (lásd IV. oszt. tankönyv 115. old.), vagyis

I = \frac{2}{3} {(\frac{2}{3})}^{2} = \frac{8}{27}

. Hasonlóképpen bizonyítható (és az affinitás alapján is következik), hogy a II terület az

E F G C

téglalap

\frac{2}{3}

része, vagyis

II = \frac{2}{3} (\frac{1}{3} \cdot \frac{1}{6}) = \frac{1}{27}

; a III pedig azonos a

B H F E

téglalappal, melynek területe

\frac{1}{3} \cdot \frac{1}{2} = \frac{1}{6}

. A kedvező terület tehát

\begin{matrix} t = I+ II+ III=\frac{8}{27}+\frac{1}{27}+\frac{1}{6}=\frac{1}{3}+\frac{1}{6}=\frac{1}{2}, \end{matrix}

és így a keresett valószínűség

\begin{matrix} V = \frac{t}{T} = \frac{1}{2} \end{matrix}

Vigassy József (Bp. I., Petőfi g. IV. o. t.)

Megjegyzés: Itt nemcsak a feladat kérdésére kaptunk feleletet, hanem arra is, hogy ha az első szakaszt találomra választjuk ki és annak hosszúsága

a

, akkor a szerkeszthetőségnek viszonylagos valószínűsége

\begin{matrix} V_{a} = - \frac{3}{2} a^{2} + 2 a . \end{matrix}

A 2. ábrán leolvasható, hogy ha

a < \frac{1}{3}

, akkor

V_{a} < \frac{1}{2}

és az

a

-val együtt

0

felé közeledik; ha

a = \frac{1}{3}

, vagy

a = 1

, akkor

V_{a} = \frac{1}{2}

vagyis, ugyanakkora, mint az abszolút valószínűség; ha pedig

\frac{1}{3} < a < 1

, akkor

\frac{1}{2} < V_{a} \leq \frac{2}{3}

, és

V_{a}

maximuma

\frac{2}{3}

, amikor

a = \frac{2}{3}

. Tehát az első szakaszt tekintve, a

≫

legkedvezőbb

≪

kiválasztás az

a = \frac{2}{3}

hosszúságú.

II. megoldás: Ismeretes, hogy a sík pontjait koordinátarendszerben számpárokkal (a pont koordinátáival) lehet megadni. Hasonló módon a tér pontjai térbeli koordinátarendszerben számhármasokkal adhatók meg. A síkbeli

x y

koordinátarendszerhez hozzáfűzzük az

O

pontban az

x y

síkra merőleges

z

tengelyt és a térbeli

P

pont

x

és

y

koordinátáján értjük az

x y

síkon fekvő merőleges vetületének,

P'

-nek a koordinátáit, míg a harmadik koordináta, a

z

koordináta a pont távolsága az

x y

síktól,

z = P' P

. Pl. a 3. ábrán szemléltetett pont:

P (5,3,7)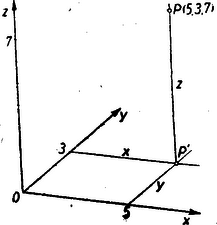

3. ábra

Mármost tekintsünk az egységnél kisebb, egyébként tetszőlegesen felvett három szakaszt egy térbeli pont három koordinátájának.

a = x

b = y

c = z

. A tér mindazon pontjai, amelyekre nézve

x < 1

y < 1

z < 1

az úgynevezett egységkocka belsejében vannak. (E kocka egyik csúcsa a kezdőpont, minden éle egységnyi és egy-egy éle az

x

y

z

tengelyre esik.) Vizsgáljuk meg, hol helyezkednek el azok a pontok, amelyek koordinátáiból háromszög szerkeszthető. Ezekre teljesülnie kell az I megoldás (1), (2), (3) feltételének, vagyis a koordináták szokásos jelölésével írva

\begin{matrix} z < x + y; & (4) \\ z > x - y; & (5) \\ z > - x + y . & (6) \end{matrix}

Egyelőre (1) helyett vizsgáljuk meg a

z = x + y

egyenlőség értelmét. (Elegendő az egységkockára szorítkoznunk. 4. ábra.)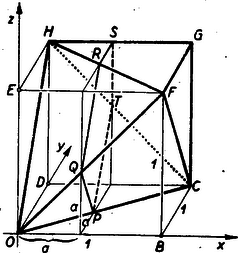

4. ábra

x z

sík pontjai közül az egyenlőségnek az origóból kiinduló

O F

lapátló pontjai tesznek eleget, az

y z

sík pontjai közül pedig a

O H

lapátló pontjai (mert pl. minden

O F

-en fekvő pontra nézve

z = x

és

y = 0

). A kocka

E F G H

lapjának pontjai közül egyenlőségünknek a

z

-t nem metsző

F H

átló pontjai tesznek eleget (

x + y = 1

és

z = 1

). Belátható továbbá, hogy a három lapátló által meghatározott

O F H

háromszög minden pontjának koordinátái kielégítik egyenletünket. Pl. vizsgáljuk meg az

F H

-val párhuzamos szakaszokat. A szakasz két végpontja feltételünknek eleget tesz. Másrészt a szakasz minden pontjára

z

azonos érték és

x + y

is azonos.^{$^{*}$}
Most már értelmet adhatunk az (1) egyenlőtlenségnek. Ennek nem tesznek eleget az egységkocka azon pontjai, amelyek az

A F H

háromszög fölött helyezkednek el, tehát az egységkockából levágott

E O F H

háromoldalú gúla pontjai, mert e pontokra nézve

z > x + y

. Hasonlóan láthatjuk be, hogy a (2) és (3) feltételt ki nem elégítő pontok szintén egy-egy (az előzővel egybevágó) három oldalú gúlát alkotnak, mégpedig a

B O C F

, illetőleg

D O C H

gúlákat. Ha az egységkockát mindhárom gúlával megcsonkítjuk, a megmaradt rész pontjai mind a három feltételnek eleget tesznek, tehát e csonkított test pontjai képviselik a kedvező eseteket. Miután pedig mindegyik gúla köbtartalma

\frac{1 \cdot 1}{2} \cdot \frac{1}{3} = \frac{1}{6}

, a három gúláé összesen:

3 \cdot \frac{1}{6} = \frac{1}{2}

, és így a keresett valószínűség

\begin{matrix} V = \frac{csonkított test köbtartalma}{egységkocka köbtartalma} = \frac{1 - \frac{1}{2}}{1} = \frac{1}{2} . \end{matrix}

Kovács László (Debrecen, Ref. g. IV. o. t.)

Megjegyzés: Ennél a megoldásnál nem kaptuk meg közvetlenül a

V_{a}

feltételes valószínűséget, de meghatározhatjuk, ha az

x = a

sik (az

y z

síkkal párhuzamos, az

x

tengelyt az origótól

x = a

távolságban metsző sík) által a megcsonkított testből kimetszett

F Q R S T

ötszög (4. ábra) területét (megfelel az 1. ábrában srafozott

t

területnek) törjük az egységkockából kimetszett egységnégyzet területével. Ezzel nemcsak az I. és II. megoldás közötti összefüggést világítottuk meg, hanem a köbtartalomnak integrállal való kiszámítását is előkészítettük.

^{$^{*}$}Megjegyezzük, hogy egy 3 ismeretlenes elsőfokú egyenlet mindig síknak az egyenlete. Mi ezúttal a síknak az egységkocka belsejébe eső részére szorítkozunk, vagyis arra a háromszögre, melyet a sík az egységkockából kimetsz.