Feladat:	619. matematika feladat	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Bártfai P. ,  Beliczky G. ,  Biczó Géza ,  Csiszár I. ,  Deres J. ,  Deseő Z. ,  Edöcsény L. ,  Eördögh L. ,  Goldstein R. ,  Grätzer Gy. ,  Holbok S. ,  Jónás J. ,  Joó F. ,  Kiss P. ,  Lackner Györgyi ,  Makkai M. ,  Marik M. ,  Mecseki A. ,  Plichta J. ,  Quittner P. ,  Rázga T. ,  Siklósi P. ,  Szabados J. ,  Szentai E. ,  Tarlacz L. ,  Tomor B. ,  Udvari A. ,  Vértes P. ,  Vigassy J. ,  Zawadowski Alfréd ,  Zsombok Z.
Füzet:	1955/február, 50 - 51. oldal		PDF  |  MathML
Témakör(ök):	Kör (és részhalmaza), mint mértani hely, Háromszögek szerkesztése, Parabola, mint mértani hely, Feladat
Hivatkozás(ok):	Feladatok: 1954/május: 619. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.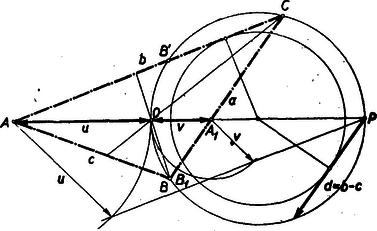   Képzeljük a feladatot megoldottnak (l. ábrát). Jelöljük az $f_a$ végpontját a $BC=a$ oldalon $A_1$-gyel. Legyen továbbá, $AO=u$, $O{A}_1=v$, $\left(u+v=f_a\right)$ és $b-c=d$. A betűzést egyébként az ábra mutatja. A szögfelezőre vonatkozó ismeretes tétel alapján, azt az $AB{A}_{1\Delta }$ $B$-ből induló és az $AC{A}_{1\Delta }$ $C$-ből induló szögfelezőjére alkalmazva, $\begin{array}{c}{\displaystyle BA:B{A}_1=u:v=CA:C{A}_1}\end{array}$ vagyis a $B$ és $C$ azon az Apollonius-féle körön vannak, amely kör pontjainak $A$-tól, ill. $A_1$-től való távolságának aránya $u:v$. E kör tehát átmegy az $O$ ponton és ‐ mivel középpontja az $A{A}_1=f_a$ egyenesen van ‐ a $B$-nek az $f_a$-ra vonatkozó tükörképe $B\text{'}$ is a körön van, és így $B\text{'}C=b-c=d$ az Apollonius-kör húrja. Eszerint a szerkesztés menete: Kiindulunk a megadott $A{A}_1=f_a$ szakaszból és az ezen ($AO=u$ révén) megadott $O$ pontból. Megszerkesztjük az $f_a$ egyenesen a $P$ pontot úgy, hogy $PA:P{A}_1=u:v$. $OP$ tehát az Apollonius-kör átmérője. E körben tetszőleges helyen megrajzolunk egy $b-c=d$ hosszúságú húrt és megszerkesztjük az Apollonius-körrel koncentrikus kört, amely ezt a húrt érinti. $A$ pontból ez utóbbi körhöz szerkesztett érintő metszi ki az Apollonius-körből a $B\text{'}$ és $C$ pontokat. $C{A}_1$ összekötése metszi ki az Apollonius-körből a keresett háromszög harmadik csúcspontját, a $B$-t. Szerkesztésünk helyességét igazoltuk, ha bebizonyítjuk, hogy $AO$ a $BAC\sphericalangle$ felezője. Mivel $B$ és $C$ az Apollonius-körön vannak, azért $BO$ felezi az $AB{A}_1\sphericalangle =ABC\sphericalangle$-et, $CO$ pedig az $AC{A}_1\sphericalangle =AC{B}_{\Delta }$-et. Az $AB{C}_{\Delta }$ e két szögfelezőjének közös pontja $O$ és így $AO$ a harmadik szögfelező. Állapítsuk meg a megoldhatóság feltételeit. Mindenekelőtt szükségképpen $u<f_a$. A beírt kör sugarát $\varrho$-val jelölve, $2\varrho <m_a$ miatt, $v<u$, vagyis $u+v=f_a<2u$, tehát $\begin{array}{c}{\displaystyle u<f_a<2u\mathrm{.}}\end{array}$ (1) Szükséges továbbá, hogy $b-c=d\le 2r$, ahol $r$ az Apollonius-kör sugara. Mivel, mint láttuk $\begin{array}{c}{\displaystyle PA:P{A}_1=\left(2r+u\right):\left(2r-v\right)=u:v\mathrm{,}}\end{array}$ amiből $\begin{array}{c}{\displaystyle 2r=\frac{2uv}{u-v}=\frac{2u\left(f_a-u\right)}{2u-f_a}\mathrm{,}}\end{array}$ azért a második feltétele a megoldhatóságnak, hogy $\begin{array}{c}{\displaystyle b-c=d\le \frac{2u\left(f_a-u\right)}{2u-f_a}}\end{array}$ (2) Biczó Géza (Bp. II., Rákóczi g. III. o. t.)   Megjegyzés: Meglehetősen hosszadalmas és komplikált megoldás: kiszámítani a beírt kör sugarát $\begin{array}{c}{\displaystyle {\varrho }^2=v^2-{\left[\frac{d\left(u-v\right)}{2u}\right]}^2\mathrm{,}}\end{array}$ majd azt megszerkeszteni. A megoldhatóság feltétele ($u>v$-n kívül) itt most, mint látható, az hogy $\frac{d\left(u-v\right)}{2u}\le v$ legyen, vagyis $d\le \frac{2uv}{u-v}$, ami egyezik az előbb nyert feltétellel.