Kezdőlap


Feladat:	617. matematika feladat	Korcsoport: 18-	Nehézségi fok: nehéz
Megoldó(k):	Balogh J. , Bártfai Pál , Biczó G. , Csanády M. , Csiszár I. , Deres J. , Deseő Z. , Edöcsény L. , Eördögh L. , Goldstein R. , Grätzer Gy. , Kálmán G. , Kiss P. , Lackner Györgyi , Makkai M. , Mecseki A. , Orosz A. , Plichta J. , Quittner P. , Rázga T. , Siklósi P. , Szeidl B. , Székely T. , Szentai E. , Tarlacz László , Udvari A. , Vértes P. , Vigassy , Zawadowski Alfréd , Zsombok Z.
Füzet:	1955/január, 23 - 25. oldal		PDF \| MathML
Témakör(ök):	Parabola egyenlete, Kúpszeletek érintői, Feladat
Hivatkozás(ok):	Feladatok: 1954/május: 617. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

1. megoldás: Felírjuk egy tetszőleges $P (u, v)$ pontból a parabolához húzható érintők egyenletét, majd annak feltételét, hogy a két érintő $45^{\circ}$ -os szöget zárjon be egymással. Így a feltételt kielégítő pontok koordinátái között összefüggést nyerünk, ez a keresett mértani hely egyenlete.
A $P (u, v)$ ponton átmenő egyenes, melynek egyenlete

\begin{matrix} y - v = m (x - u) \end{matrix}

(1)

alakú, ez esetben érinti az

\begin{matrix} y^{2} = 2 p x \end{matrix}

(2)

parabolát, ha a parabolával alkotott két metszéspontja egybeesik. Fejezzük ki (l)-ből

x

-et, és a nyert értéket írjuk be (2)-be, akkor rendezés után a következő egyenlethez jutunk:

\begin{matrix} m y^{2} - 2 p y + (2 p v - 2 m p u) = 0. \end{matrix}

y

-ra nézve egybeeső gyököket akkor kapunk, ha az egyenlet diszkriminánsa

\begin{matrix} 4 p^{2} - 8 m p v + 8 m^{2} p u = 0, \end{matrix}

azaz egyszerűsítve és rendezve

\begin{matrix} 2 u m^{2} - 2 v m + p = 0. \end{matrix}

Ezt az egyenletet

m

-re megoldva nyerjük a

P (u, v)

pontból a parabolához húzható két érintő iránytényezőjét.

\begin{matrix} m_{1} = \frac{v + \sqrt[]{v^{2} - 2 p u}}{2 u} és m_{2} = \frac{v - \sqrt[]{v^{2} - 2 p u}}{2 u} \end{matrix}

(3)

Annak feltétele, hogy a két érintő

45^{\circ}

-os szöget zárjon be egymással

\begin{matrix} tg 45^{\circ} = 1 = \frac{m_{1} - m_{2}}{1 + m_{1} m_{2}}, ebből 1 + m_{1} m_{2} = m_{1} - m_{2} \end{matrix}

(4)

Ez utóbbi egyenletbe behelyettesítve

m_{1}

és

m_{2}

-nek a (3) egyenletekből nyert értékét, megkapjuk a keresett mértani hely egyenletét:

\begin{matrix} 1 + \frac{v + \sqrt[]{v^{2} - 2 p u}}{2 u} \cdot \frac{v - \sqrt[]{v - 2 p u}}{2 u} = \frac{v + \sqrt[]{v^{2} - 2 p u}}{2 u} - \frac{v - \sqrt[]{v^{2} - 2 p u}}{2 u}, \end{matrix}

azaz összevonva

\begin{matrix} 1 + \frac{p}{2 u} = \frac{\sqrt[]{v^{2} - 2 p u}}{u} . \end{matrix}

Az egyenletet át fogjuk alakítani, hogy megállapíthassuk, milyen másodrendű görbe egyenlete és melyek e görbe jellemző adatai. Végigszorozzuk

u

-val, négyzetre emelünk, majd az

u

-t tartalmazó tagokat kiegészítjük teljes négyzetté

\begin{matrix} {(u + \frac{3}{2} p)}^{2} - v^{2} = 2 p^{2}, azaz \frac{{(u + \frac{3}{2} p)}^{2}}{2 p^{2}} - \frac{v^{2}}{2 p^{2}} = 1. \end{matrix}

Ez egyenlő oldatú hiperbola egyenlete. A hiperbola főtengelye egybeesik a parabola tengelyével, középpontja az

O (- \frac{3 p}{2},0)

és féltengelyeinek hossza

a = b = p \sqrt[]{2}

. A lineáris excentricitás

c = \sqrt[]{a^{2} - b^{2}} = a \sqrt[]{2} = 2 p

, vagyis a hiperbola egyik fókusza

F_{2} (\frac{p}{2},0)

egybeesik a parabola

F

fókuszával (l. ábrát).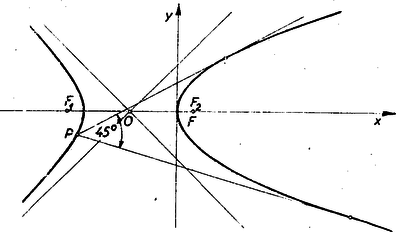

A keresett mértani hely nem az egész hiperbola, hanem annak csak a parabolától távolabb eső ága. A másik ág pontjaiból a parabola

135^{\circ}

-os szög alatt látszik. Ugyanis az átalakításnál négyzetre emeltünk és ezáltal egybeolvasztottuk az

\begin{matrix} 1 = \frac{m_{1} - m_{2}}{1 + m_{1} m_{2}} egyenletet a - 1 = \frac{m_{1} - m_{2}}{1 + m_{1} m_{2}} \end{matrix}

egyenlettel. Az utóbbi egyenlet viszont azt fejezi ki, hogy a két érintő egymással

135^{\circ}

-os szöget zár be.

Tarlacz László (Szombathely, Nagy Lajos g. III. o. t.)

II. megoldás: Legyen a

P (x, y)

a keresett mértani hely egy pontja, akkor e pontból a parabolához húzható érintők

45^{\circ}

-os szöget zárnak be. Valamely

P (x_{1}, y_{1})

pontban a parabola érintőjének egyenlete

\begin{matrix} y_{1} y - p (x_{1} + x) = 0. \end{matrix}

Mivel az érintési pont a parabolán fekszik, azért

y_{1}^{2} - 2 p x_{1} = 0

, és így az érintő egyenlete így is írható

\begin{matrix} y_{1}^{2} - 2 y y_{1} + 2 p x = 0, \end{matrix}

amely egyenletet

y_{1}

-re megoldva

\begin{matrix} y_{1} = \pm \sqrt[]{y^{2} - 2 p x .} \end{matrix}

Tehát a

P (x, y)

pontból a parabolához húzható érintők érintési pontjainak ordinátái

\begin{matrix} y_{1} = y + \sqrt[]{y^{2} - 2 p x}, y_{2} = y - \sqrt[]{y^{2} - 2 p x} . \end{matrix}

Az érintők iránytangensei

\begin{matrix} m_{4} = \frac{p}{y_{1}}, illetve m_{2} = \frac{p}{y_{2}}, \end{matrix}

tehát a két egyenes szögének tangensét kifejező képlet alapján nyerjük

\begin{matrix} 1 = \frac{p y_{1} - p y_{2}}{y_{1} y_{2} + p^{2}} = \frac{2 \sqrt[]{y^{2} - 2 p x}}{2 x + p} . \end{matrix}

Innen a keresett mértani hely egyenlete

\begin{matrix} 4 x^{2} - 4 y^{2} + 12 p x + p^{2} = 0 \end{matrix}

Ez azonban így is írható:

\begin{matrix} {(x + \frac{3 p}{2})}^{2} - y^{2} - 2 p^{2} = 0, \end{matrix}

ami egyezik az első megoldásban nyert eredménnyel.

Bártfai Pál (Bp. I. Petőfi g. III. o. t.)