Kezdőlap


Feladat:	598. matematika feladat	Korcsoport: 18-	Nehézségi fok: nehéz
Megoldó(k):	Bártfai Pál , Plichta Jenő
Füzet:	1954/november, 120 - 122. oldal		PDF \| MathML
Témakör(ök):	Fizikai jellegű feladatok, Szélsőérték-feladatok differenciálszámítás nélkül, Hajítások, Függőleges hajítás, Feladat
Hivatkozás(ok):	Feladatok: 1954/március: 598. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás: Nyilvánvaló, hogy a két mozgás egy és ugyanazon függőleges síkban történik. Ha e síkban $x$ tengelynek vesszük a ferdén hajított test vetületét a vízszintes síkon, kezdőpontnak a $A$ pontot, akkor a fizikából ismeretes, hogy a közös elhajítási időponttól számított $t$ másodperc múlva az első test koordinátái

\begin{matrix} x_{1} = c t cos α, y_{1} = c t sin α - \frac{g}{2} t^{2}, \end{matrix}

a második test koordinátái pedig

\begin{matrix} x_{2} = a y_{2} = c t - \frac{g}{2} t^{2}, \end{matrix}

és így a két test távolságának négyzete

\begin{matrix} d^{2} = {(x_{1} - x_{2})}^{2} + {(y_{1} - y_{2})}^{2} = {(c t cos α - a)}^{2} + {(c t sin α - c t)}^{2} = \\ = c^{2} t^{2} cos^{2} α - 2 a c t cos α + a^{2} + c^{2} t^{2} sin^{2} α - 2 c^{2} t^{2} sin α + c^{2} t^{2} = \\ = 2 c^{2} t^{2} (1 - sin α) - 2 a c t cos α + a^{2} . & (1) \end{matrix}

t

-re nézve másodfokú függvény, melynek ‐ mivel

t^{2}

együtthatója

2 c^{2} (1 - sin α) > 0

‐ minimuma van a

\begin{matrix} t_{0} = - \frac{- 2 a c cos α}{2 \cdot 2 c^{2} (1 - sin α)} = \frac{a cos α}{2 c (1 - sin α)} \end{matrix}

helyen.
A

d^{2}

minimális értékét megkapjuk, ha a

t_{0}

értékét behelyettesítjük az (1) alatti függvénybe:

\begin{matrix} d_{min}^{2} = \frac{a^{2} cos^{2} α}{2 (1 - sin α)} - \frac{a^{2} cos^{2} α}{1 - sin α} + a^{2} = a^{2} - \frac{a^{2} cos^{2} α}{2 (1 - sin α)} = \\ = a^{2} (1 - \frac{1 - sin^{2} α}{2 (1 - sin α)}) = a^{2} (1 - \frac{1 + sin α}{2}) = a^{2} \frac{1 - sin α}{2}, \end{matrix}

vagyis

\begin{matrix} d_{min} = a \sqrt[]{\frac{1 - sin α}{2}} . \end{matrix}

Figyeljük meg, amíg a

t_{0}

értéke még függ a

c

közös kezdősebességtől, a

d_{min}

már

c

-től független.
Az adott értékekkel

\begin{matrix} d_{min} = 50 \sqrt[]{3} \sqrt[]{\frac{1 - \frac{1}{2}}{2}} = 25 \sqrt[]{3} m . \end{matrix}

Plichta Jenő (Mezőkövesd, I. László g. IV. o. t.)

II. megoldás: A nehézségi erő mindkét testnek egyenlő függőleges irányú gyorsulást ad, és ezáltal egyenlő függőleges irányú eltolódást okoz, ami viszont a két testnek egymástól való távolságát nem befolyásolja, és így feladatunknál a nehézségi erőtől eltekinthetünk. Tehát az

A B H

derékszögű háromszög (lásd ábrát)

A H = p

átfogóján és

B H = q

befogóján egyaránt

c

sebességgel haladó testek távolságának minimumát vizsgáljuk. A mozgás kiindulása

A

és

B

-ből egyidejű.

t

idő múlva az átfogón mozgó test

A'

-be, a befogón mozgó test

B'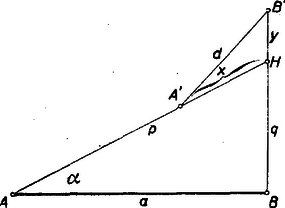

-be ér.

A A' = B B' = c t

Tekintsük változónak az

\begin{matrix} x = p - c t, y = c t - q \end{matrix}

mennyiségeket. Ez esetben

x + y = p - q

állandó.
Nyilvánvaló, hogy amíg

x > 0

, és

y < 0

, addig

t

növekedésével az

A' B' = d

távolság fogy, és

x < 0

y > 0

esetén pedig

t

növekedésével

d

is növekszik (mégpedig minden határon túl), tehát minimum csak

x > 0

y > 0

esetén lehet.
Ez esetben a cosinustétel értelmében

\begin{matrix} d^{2} = x^{2} + y^{2} - 2 x y cos (90^{\circ} + α) = x^{2} + 2 x y + y^{2} - 2 x y + 2 x y sin α = \\ = {(x + y)}^{2} - 2 x y (1 - sin α) . & (1) \end{matrix}

Mivel

x + y

állandó, azért

d^{2}

akkor lesz minimális (figyelembe véve, hogy

1 - sin α > 0

), ha

x y

maximális. Ha két mennyiség összege állandó, a mértani közép akkor maximális, ha a két mennyiség egyenlő. Tehát

x y

akkor maximális, ha

x = y

, vagyis

x + y = 2 x = p - q

, azaz

x = y = \frac{p - q}{2}

.
Most kiszámíthatjuk a

t_{0}

értékét, annak alapján, hogy

p - c t_{0} = c t_{0} - q

vagyis

t_{0} = \frac{p + q}{2 c}

, de inkább megmutatjuk, hogy az I. megoldástól eltérően

t_{0}

kiszámítása nélkül is meghatározhatjuk

d_{min}

értékét.
Ugyanis (1) alapján

\begin{matrix} d_{min}^{2} = {(p - q)}^{2} - \frac{{(p - q)}^{2}}{2} (1 - sin α) = \frac{{(p - q)}^{2}}{2} + \frac{{(p - q)}^{2}}{2} sin α = \\ = \frac{{(p - q)}^{2}}{2} (1 + sin α) . & (2) \end{matrix}

Mivel

p = \frac{a}{cos α}

és

q = a tg α

, azért

\begin{matrix} p - q = \frac{a}{cos α} - \frac{a sin α}{cos α} = \frac{a (1 - sin α)}{cos α} \end{matrix}

és így (2) alapján

\begin{matrix} d_{min}^{2} = \frac{a^{2} {(1 - sin α)}^{2}}{2 cos^{2} α} (1 + sin α) = \frac{a^{2} (1 - sin^{2} α) (1 - sin α)}{2 cos^{2} α} = \frac{a^{2} (1 - sin α)}{2}, \end{matrix}

ahonnan

\begin{matrix} d_{min} = a \sqrt[]{\frac{1 - sin α}{2}} . \end{matrix}

Bártfai Pál (Bp., I., Petőfi g. III. o. t.)