Kezdőlap


Feladat:	595. matematika feladat	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Almási Lajos , Bártfai P. , Bauer A. , Biczó J. , Bonyhárd P. , Boros P. , Csanády M. , Cser T. , Csiszár I. , Deseő Z. , Edöcsény L. , Eördögh L. , Fuchs T. , Goldstein R. , Holbok S. , Kálmán Gy. , Katona P. , Kirz J. , Kovács L. , Krammer G. , Lackner Györgyi , Makkai M. , Mecseki A. , Orlik P. , Parlagh Gy. , Perneczky L. , Pintér L. , Quittner P. , Rácz M. , Rázga T. , Rédl Gy. , Roboz Ágnes , Rozsondai Z. , Solymoss O. , Spellenberg S. , Szentai E. , Tomor B. , Tranta F. , Uray L. , Vigassy J. , Zawadowski Alfréd , Zsombok Z.
Füzet:	1954/november, 115 - 117. oldal		PDF \| MathML
Témakör(ök):	Geometriai valószínűség, Feladat
Hivatkozás(ok):	Feladatok: 1954/február: 595. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

A keresett valószínűség attól függ, hogy milyen mennyiségekkel jellemezzük a két tetszés szerint kiválasztott pont helyzetét; különböző mennyiségek alapul választásának pedig az felel meg, hogy különböző eseményeket tekintünk egyenlően valószínűnek.

I. megoldás: Legyen a félkör sugara

r

és jelöljük a félkörív két végpontját

A

ill.

B

-vel

(\hat{A B} = r π)

, a két mozgó pontot

C

- ill.

D

-vel, és legyen

\hat{A C} = x

\hat{A D} = y

.
Történjék a tetszőleges pont kiválasztása úgy, hogy

x

és

y

gyanánt tetszőlegesen választunk két értéket

0

és

r π

között.
A derékszögű koordináta rendszerben az összes lehetséges

x

y

értékek beborítják a

(0, 0)

(0, r π)

(r π, r π)

és

(r π, 0)

pontok által alkotott négyzetet (1. ábra).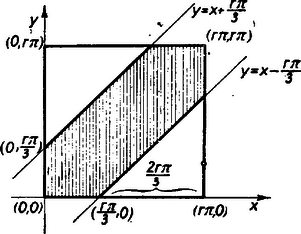

1. ábra

Kedvezőek ezek közül csak azok a pontok, amelyekre nézve

| x - y | \leq \frac{r π}{3}

, vagyis

x - \frac{r π}{3} < y < x + \frac{r π}{3}

. (Az 1. ábrán a sraffozott terület.) A keresett valószínűség tehát

\begin{matrix} v_{1} = \frac{r^{2} π - {(\frac{2 r π}{3})}^{2}}{r^{2} π^{2}} = 1 - \frac{4}{9} = \frac{5}{9} \approx 0, 556. \end{matrix}

Almási Lajos (Bp., II., Rákóczi g. III. o. t.)

Megjegyzés: Jelen feladat átfogalmazható a VI. kötet 103. oldalán (1953 április) tárgyalt 1. sz. példára.

Roboz Ágnes (Bp., VI., Varga Katalin lg. III. o. t.)

II. megoldás: A körív két pontja húrt határoz meg, és minden húr a felezőpontja által egyértelműen meg van határozva, tehát a húrfelezőpontokat választjuk ki tetszőlegesen, és kedvezőek azok az esetek, amelyekben a húr nem nagyobb a sugárnál.
Először meg kell határozni az összes lehetséges húrfelezőpontok mértani helyét, vagyis azokat a pontokat az

A \hat{B A}

félkörlap belsejében, amelyekhez tartozó húr végpontjai egyáltalán rajta vannak, az

\hat{A B}

félköríven. Az

A

illetőleg

B

pontokból kiinduló és a félkörlapon belül fekvő húrok felezőpontjainak mértani helye az

A O

ill.

O B

körsugarak fölé rajzolt félkörök. (Az

\hat{A B}

félkörnek

1 : 2

arányú kicsinyítése az

A

illetőleg

B

hasonlósági centrumból.) Az

\hat{A O}

\hat{O B}

és

\hat{A B}

félkörök által határolt idom pontjai képviselik tehát az összes lehetséges húrfelezőpontokat (2. ábra).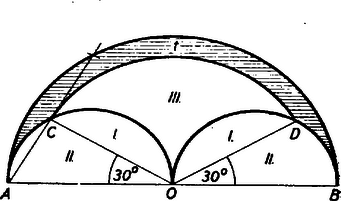

2. ábra

\hat{A B}

körívben rajzolt

r

hosszúságú húrok olyan körívet burkolnak, amelynek sugara nyilván a húrfelezőpontnak távolsága az

O

ponttól, vagyis (az

A O C

derékszögű háromszögből)

\frac{r}{2} \sqrt[]{3}

. A húrfelezőpontra nézve tehát kedvezők mindazok a pontok, amelyek az

r

és

\frac{r}{2} \sqrt[]{3}

sugarú körök által meghatározott körgyűrűben és a fenti három körív által határalt

t

idomban vannak. (A 2. ábrában a sraffozott terület.)
A >>lehetséges terület<< tehát

\begin{matrix} T = \frac{r^{2} π}{2} - {(\frac{r}{2})}^{2} π = \frac{r^{2} π}{4} . \end{matrix}

A 2. ábra szerinti betűzésben

\begin{matrix} 2 \cdot I + 2 \cdot II + III + t = \frac{r^{2} π}{2} . \end{matrix}

(1)

O \hat{C D} O

körcikknek szöge

180^{\circ} - 2 \cdot 30^{\circ} = 120^{\circ}

, sugara pedig (mint láttuk)

\frac{r}{2} \sqrt[]{3}

, és így

\begin{matrix} 2 \cdot I + III = \frac{{(\frac{r}{2} \sqrt[]{3})}^{2} π}{3} = \frac{r^{2} π}{4}, \end{matrix}

(2)

továbbá

\begin{matrix} 2 \cdot I + 2 \cdot II = \frac{r^{2} π}{4} . \end{matrix}

(3)

(2) és (3) összegét kivonva (1)-ből

\begin{matrix} t - 2 \cdot I = 0, \end{matrix}

vagyis

\begin{matrix} t = 2 \cdot I = 2 \cdot \frac{1}{3} (\frac{r^{2} π}{4} - \frac{3 r^{2} \sqrt[]{3}}{16}) = r^{2} (\frac{π}{6} - \frac{\sqrt[]{3}}{8}) \end{matrix}

és így a keresett valószínűség

\begin{matrix} v_{2} = \frac{t}{T} = \frac{r^{2} (\frac{π}{6} - \frac{\sqrt[]{3}}{8})}{r^{2} \frac{π}{4}} = \frac{4 π - 3 \sqrt[]{3}}{6 π} \approx \frac{7, 3702}{6 π} \approx 0, 391. \end{matrix}

Lackner Györgyi (Bp., V., Fonóip. techn. III. o. t.)