Kezdőlap


Feladat:	592. matematika feladat	Korcsoport: 18-	Nehézségi fok: nehéz
Megoldó(k):	Balatoni F. , Balogh J. , Bártfai P. , Beke Gy. , Biczó G. , Csanády M. , Csiszár I. , Grätzer Gy. , Joó F. , Lackner Györgyi , Makkai M. , Németh L. , Orosz A. , Ott L. , Plichta J. , Quittner P. , Rázga T. , Rozsondai Z. , Solymoss O. , Szentai E. , Tomor B. , Vértes B. , Zawadowski Alfréd , Zsombok Z.
Füzet:	1954/november, 111 - 112. oldal		PDF \| MathML
Témakör(ök):	Beírt gömb, Gúlák, Feladat
Hivatkozás(ok):	Feladatok: 1954/február: 592. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Jelöljük a két koncentrikus gömb közös középpontját $O$ -val. A gúlalapok ‐ mivel érintik az $O$ középpontú beírt gömböt, vagyis egyenlő távolságnyira vannak $O$ -tól ‐ egybevágó körlapokat metszenek ki a köréírt gömbből. A gúlalapok köré írt körük sugara tehát egyenlő, és e köröknek középpontjai $(K_{1}$ , $K_{2}$ , $K_{3}$ , $K_{4}$ ) egyben a beírt gömb érintési pontjai. Tehát $O K_{1} = O K_{2} = O K_{3} = O K_{4}$ szakaszok rendre merőlegesek a gúlalapokra (1. ábra).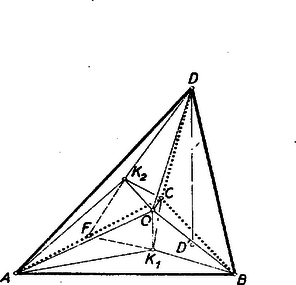

1. ábra

Egyenlő sugarú körökben egyenlő húrokhoz egyenlő kerületi szögek tartoznak, amiből következik, hogy ha az

A B C ▵

szögeit

α

β

γ

-val jelöljük, akkor a

D

csúcsnál levű élszögek is

α

β

γ

, és így ezeknek összege

180^{\circ}

. Ami a

D

csúcsra áll, az teljesen ugyanúgy kimutatható bármely csúcsra. Ebből következik, hogy mind a négy háromszögben a szögek:

α

β

γ

. Mivel a körülírt kör sugara ‐ mint láttuk ‐ mind a négy háromszögben egyenlő, azért a négy háromszög egybevágó.
Három élszög csak úgy alkothat triédert, ha a legnagyobb élszög is kisebb a másik kettő összegénél. Jelen esetben a 3 élszög összege

180^{\circ}

, tehát a legnagyobb élszög szükségképpen kisebb a derékszögnél, vagyis a négy egybevágó háromszög szükségképpen hegyesszögű.
Ezek szerint, ha a

D

csúcspontban összefutó 3 gúlalapot az

A B C

alaplap oldalai körül az alaplap síkjába forgatjuk, akkor a gúlának a 2. ábrában feltüntetett hálózatát nyerjük. (E hálózatból az is világosan leolvasható, hogy a gúla kitérő élei egyenlők.)
Még meg kell mutatnunk, hogy az eddig megállapított szükséges feltételek elégségesek is, vagyis ha egy tetszőleges

A B C

hegyesszögű háromszög csúcspontjain át párhuzamosakat húzunk a szemközti oldalakkal, az így nyert

D_{1} D_{2} D_{3}

háromszögben fekvő négy egybevágó háromszög (2. ábra) tényleg egy háromoldalú gúla hálózata és az így nyert gúla eleget tesz a kiszabott feltételeknek.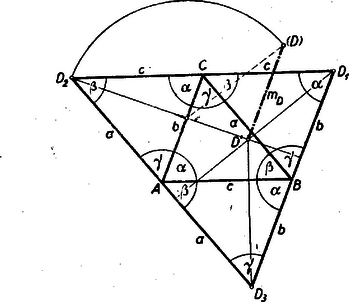

2. ábra

Ha az

A B C ▵

a

és

b

oldalai körül felhajtjuk a

D_{1}

ill.

D_{2}

csúcspontú gúlalapokat, amíg

D_{1}

és

D_{2}

egy térbeli

D

pontban egybeesik (ez elérhető, mivel

C D_{1} = C D_{2}

), akkor nyilván a

D

gúlacsúcspont merőleges vetülete az

A B C

alapsíkon

D'

nem egyéb, mint a

D_{1} D_{2} D_{3} ▵

magasságpontja. Az így nyert

D A B ▵ ≃ D_{3} A B ▵

, és ha az utóbbit felhajtjuk

A B = c

körül, a

D_{3}

pont is egybeesik a

D

ponttal, mivel a harmadik magasságvonal szükségképpen átmegy a magassági ponton. (Az ábrán még megszerkesztettük a gúla

D' (D)

magasságát is.)
A megszerkesztett gúla 4 oldalháromszöge köré egyenlő sugarú körök írhatók. Ezeknek, 3‐3 pontja a tetraéder köré írt gömbön van, tehát a négy kör teljes egészében is. De egy gömbön levő egyenlő sugarú körök középpontjai egyenlő távolságra vannak a gömb középpontjától és éppen a gömb középpontjából a körök síkjára bocsátott merőlegesek talppontjai. Tehát a körért gömb középpontja egyszersmind a határlapokat érintő, beírt gömb középpontja is.