Kezdőlap


Feladat:	590. matematika feladat	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Bártfai Pál , Edöcsény László
Füzet:	1954/november, 109 - 110. oldal		PDF \| MathML
Témakör(ök):	Szögfüggvények, síkgeometriai számítások, Feladat
Hivatkozás(ok):	Feladatok: 1954/február: 590. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás: Kössük össze az $O_{2}$ pontot a $B$ -vel és húzzuk meg a másik körben az $O_{2} B$ sugárral párhuzamos $O_{1} C$ sugarat (1. ábra).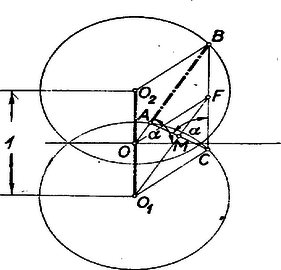

1. ábra

Mivel

O_{1} C = O_{2} B = r

és

O_{1} C ∥ O_{2} B

, azért

O_{1} O_{2} B C

paralelogramma, és így

B C ∥ O_{1} O_{2}

és

B C = O_{1} O_{2} = 1

.
Ha

B C

felezőpontját

F

-fel jelöljük, akkor

O_{1} F ∥ O B

.
Kössük össze a

C

pontot

A

-val és legyen a

C A

és

O_{1} F

metszéspontja

M

. Mivel

C F = F B

, azért

C M = M A

, vagyis

O_{1} F

felezi az

A C

húrt, de a kör középpontján és a húrfelezőponton átmenő egyenes merőleges a húrra, tehát

O_{1} F ⊥ A C

, vagyis (mivel

O_{1} F ∥ O B

)

\begin{matrix} A C ⊥ O B . \end{matrix}

A B C

derékszögű háromszögben a

C ∢ = α

, mint merőlegesszárú szög és így

\begin{matrix} A B = B C sin α = sin α, \end{matrix}

függetlenül az

r (> \frac{1}{2})

sugártól.

Edöcsény László (Bp., XI., József Attila g. III. o. t.)

II. megoldás: A betűzést a 2. ábra mutatja.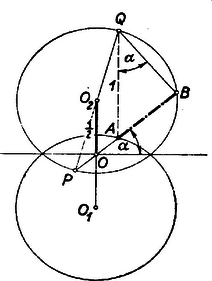

2. ábra

Messe a félegyenes meghosszabbítása az

O_{2}

középpontú kört egy

P

pontban, akkor

P

A

pontnak centrális tükörképe az

O

pontra nézve, tehát

P O = O A

.
A

P

pontból nagyítsuk fel az

O O_{2}

szakaszt

2 : 1

arányban, nyerjük az

O O_{2}

-vel párhuzamos

A Q = 2 \cdot O O_{2} = 2 \cdot \frac{1}{2} = 1

szakaszt. Az

A B Q ▵

-ben a

B ∢

Thales tétele értelmében derékszög, a

Q ∢

pedig mint merőlegesszárú szög egyenlő

α

-val. Az

A B Q

derékszögű háromszögben tehát

\begin{matrix} A B = A Q sin α = sin α . \end{matrix}

Bártfai Pál (Bp., I., Petőfi g. III. o. t.)