Kezdőlap


Feladat:	586. matematika feladat	Korcsoport: 18-	Nehézségi fok: nehéz
Megoldó(k):	Ambrus G. , B. Nagy Kornélia , Bagi A. , Bárdos A. , Bauer A. , Beke Éva , Beke Mária , Beliczky G. , Erdős S. , Fuchs T. , Gergely P. , Goldstein R. , Grätzer Gy. , Holbok S. , Kálmán Gy. , Kirz J. , Kovács J. , Lackner Györgyi , Masszi Gy. , Mecseki A. , Ott L. , Pátkai Gy. , Plichta J. , Roboz Ágnes , Rozsondai Z. , Solymoss O. , Szeidl B. , Székely T. , Szentai E. , Tóth P. , Tranta F.
Füzet:	1954/október, 55 - 56. oldal		PDF \| MathML
Témakör(ök):	Gömbi geometria, Terület, felszín, Feladat
Hivatkozás(ok):	Feladatok: 1954/január: 586. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Legyen a változó gömb sugara $K O = ϱ$ . A két gömb $K O$ centrális egyenesén átfektetett minden sík a két gömbből egy-egy főkört metsz ki, melyeknek közös húrja legyen $A B = h$ (lásd ábrát).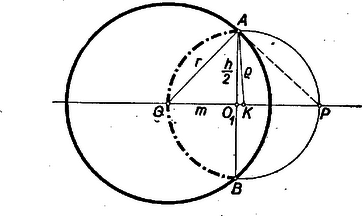

E két főkörnek a

K O

tengely körüli forgásából keletkezik a két gömb, és az

A

(ill.

B

) pont forgásából pedig a két gömb közös (áthatási) görbéje: az

O_{1}

középpontú,

\frac{h}{2}

sugarú kör. A változó

K

középpontú és

ϱ

sugarú gömbnek az adott szilárd gömbbe eső része, tehát e kör által határolt gömbsüveg, melynek magassága

O_{1} O = m

és felszíne legyen

F

. Ha a változó gömbben az

O

pontnak átellenes pontját

P

-vel jelöljük, akkor a Thales-tétel értelmében

O A P ▵

-ben az

A ∢

derékszög.
Ismert tétel alapján

\begin{matrix} O A^{2} = O P \cdot O O_{1}, vagyis r^{2} = 2 ϱ \cdot m, \end{matrix}

amiből

\begin{matrix} m = \frac{r^{2}}{2 ϱ}, \end{matrix}

és így a gömbsüveg ismert felszínképletét felhasználva

\begin{matrix} F = 2 ϱ π \cdot m = 2 ϱ π \cdot \frac{r^{2}}{2 ϱ} = r^{2} π . \end{matrix}

Látjuk tehát, hogy a szilárd

r

sugarú gömbbe eső

F

területrész egy

ϱ

-tól, tehát a

K

pont helyzetétől, független állandó.
Határesetek: a) Ha

ϱ = \frac{r}{2}

, akkor a változó gömb, belülről érintve az adott szilárd gömböt, teljesen annak belsejébe esik. Tehát a kérdéses felület ez esetben

\begin{matrix} F = 4 ϱ^{2} π = 4 {(\frac{r}{2})}^{2} π = r^{2} π . \end{matrix}

b) Ha

ϱ

minden határon túl megnő, akkor a változó sugarú gömb egy, az

O

ponton átmenő és az

O K

irányra merőleges síkká fajul, a közös rész pedig a sík által kimetszett

r

sugarú főkörmetszet, amelynek területe szintén

r^{2} π

B. Nagy Kornélia (Tiszaföldvár, Hajnóczy g. IV. o. t.)