Kezdőlap


Feladat:	582. matematika feladat	Korcsoport: 18-	Nehézségi fok: nehéz
Megoldó(k):	Bártfai Pál , Bauer A. , Kálmán Gy. , Lackner Györgyi , Reichlin-M V. , Rozsondai Z. , Szuromi L. , Tomor B. , Uray L. , Zawadowski Alfréd , Zsombok Z.
Füzet:	1954/október, 50 - 51. oldal		PDF \| MathML
Témakör(ök):	Sorozat határértéke, Feladat
Hivatkozás(ok):	Feladatok: 1954/január: 582. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Helyettesítsünk $n = m^{3}$ -t, kapjuk

\begin{matrix} F = m^{4} sin \frac{π}{m} \sqrt[]{\frac{1}{m^{6}} + sin^{4} \frac{π}{m}} = \\ = m sin \frac{π}{m} \sqrt[]{1 + m^{6} sin^{4} \frac{π}{m}} > m sin \frac{π}{m} m^{3} sin^{2} \frac{π}{m}, \end{matrix}

azaz

\begin{matrix} F > m {(m sin \frac{π}{m})}^{3} . \end{matrix}

(1)

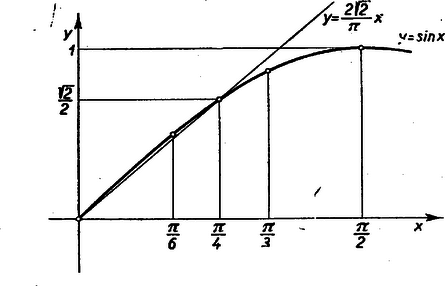Mint a cikkben, most is

\frac{π}{m}

helyébe

\frac{π}{m}

olyan többszörösét kell írni, amely kisebb mint

sin \frac{π}{m}

, legalább ha

m

elég nagy. Ha az

y = sin x

görbében megrajzoljuk azt a húrt, amely átmegy a nulla és

\frac{π}{4}

abszcisszájú pontokon, vagyis a

(0, 0)

és

(\frac{π}{4}, \frac{\sqrt[]{2}}{2})

pontokon (l. ábrát), akkor ‐ figyelembe véve, hogy a

sin

görbe

(0, \frac{π}{4})

intervallumban alulról konkáv ‐ az

y = \frac{2 \sqrt[]{2}}{π} x

egyenlettel megadott húr pontjai a

(0, \frac{π}{4})

intervallumban a sinusgörbe pontjai alatt vannak, vagyis ha

0 < x < \frac{π}{4}

, akkor

sin x > \frac{2 \sqrt[]{2}}{π} x

, azaz, ha

m > 4

, akkor

sin \frac{π}{m} > \frac{2 \sqrt[]{2}}{π} \frac{π}{m} = \frac{2 \sqrt[]{2}}{m}

. Tehát (1) alapján

\begin{matrix} F > m {(2 \sqrt[]{2})}^{3} = 16 \sqrt[]{2} m \end{matrix}

feltéve, hogy

m > 4

.
Mivel

16 \sqrt[]{2} m > 100

, ha

m > \frac{100}{16 \sqrt[]{2}} \sim 4, 42

és

16 \sqrt[]{2} m > 1 000 000

, ha

m > 10 000 \cdot 4, 42 = 44 200

, azért a keresett küszöbszámokul megfelelnek

\begin{matrix} μ_{100} = 5 és μ_{1 000 000} = 44 200. \end{matrix}

Megjegyzés: Utóbbi küszöbszámra kisebb értéket nyerhetünk, hogy ha a

(0, \frac{π}{4})

intervallum helyett kisebb intervallumot választunk. Pl. a

(0, \frac{π}{12})

intervallum esetén

μ_{1 000 000} = 33 445

adódik.

Bártfai Pál (Bp., I., Petőfi g. III. o. t.)