Kezdőlap


Feladat:	565. matematika feladat	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Almási L. , Bártfai P. , Bauer A. , Beke Gy. , Beliczky G. , Biczó Géza , Bonyhárd P. , Csiszár I. , Edöcsény L. , Frivaldszky J. , Gergely P. , Kiss P. , Kovács L. , Krammer G. , Molnár K. , Papp Z. , Pátkai Gy. , Quittner Pál , Rázga T. , Solymoss O. , Szegő J. , Szendrei I. , Tolnai T. , Uray L. , Varga J. , Vigassy J. , Zawadowski Alfréd
Füzet:	1954/április, 121 - 122. oldal		PDF \| MathML
Témakör(ök):	Trigonometriai azonosságok, Feladat
Hivatkozás(ok):	Feladatok: 1953/november: 565. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás: A baloldalon szereplő gyök alatti mennyiség az $α = 90^{\circ} \pm k \cdot 360^{\circ} (k = 0,1,2, ...)$ értékek kivételével mindenütt értelmezve van és értéke seholsem negatív.
Ha a gyököt pozitív előjellel tekintjük, akkor az azonosság csak azokra az $α$ értékekre állhat fenn, amelyekre $45^{\circ} + \frac{α}{2}$ az I. és III. szögnegyedben van.
A baloldalt átalakítjuk:

\begin{matrix} \sqrt[]{\frac{1 + sin α}{1 - sin α}} = \sqrt[]{\frac{sin 90^{\circ} + sin α}{sin 90^{\circ} - sin α}} = \sqrt[]{\frac{2 sin (45^{\circ} + \frac{α}{2}) cos (45^{\circ} - \frac{α}{2})}{2 cos (45^{\circ} + \frac{α}{2}) sin (45^{\circ} - \frac{α}{2})}} . \end{matrix}

(1)

Mivel az

\frac{α}{2} = 45^{\circ} \pm k \cdot 180^{\circ} (k = 0,1,2, ...)

értékek kizártak, az (1) alatti kifejezés:

\begin{matrix} \sqrt[]{tg (45^{\circ} + \frac{α}{2}) cotg (45^{\circ} - \frac{α}{2})} = \sqrt[]{{tg}^{2} (45^{\circ} + \frac{a}{2})} = tg (45^{\circ} + \frac{α}{2}) . \end{matrix}

45^{\circ} + \frac{α}{2}

a II. ill. IV. szögnegyedben van, akkor a négyzetgyökök előjelei megfelelőképpen veendők.

II. megoldás: Az egységsugarú körben (l. ábrát), legyen az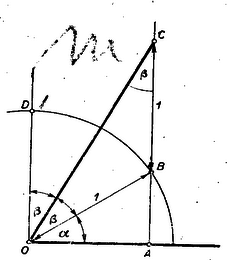

A O B ∢ = α

O B = 1

A B = sin α

O A = cos α

A B

távolságot hosszabbítsuk meg

B

-n túl

B C = 1

-gyel. Az

O C B ∢

-et

β

-val jelölve, a

B O C ∢

is egyenlő

β

-val, mert az

O B C

háromszög egyenlőszárú. A

C O D ∢ = β

, mint váltószög, ha

D O ⊥ O A

.
Tehát

2 β + α = 90^{\circ}

, vagyis

\begin{matrix} β = \frac{90^{\circ} - α}{2} = 45^{\circ} - \frac{α}{2}, és így α + β = 45^{\circ} + \frac{α}{2} . \end{matrix}

O A C

derékszögű háromszögben

\begin{matrix} tg (α + β) = tg (45^{\circ} + \frac{α}{2}) = \frac{1 + A B}{O A} = \\ = \frac{1 + A B}{\sqrt[]{1 - A B^{2}}} = \sqrt[]{\frac{{(1 + A B)}^{2}}{(1 + A B) (1 - A B)}} = \sqrt[]{\frac{1 + A B}{1 - A B}} = \sqrt[]{\frac{1 + sin α}{1 - sin α}} . \end{matrix}

Ez a bizonyítás a többi térnegyedre is kiterjeszthető.

Biczó Géza (Bp., II., Rákóczi g. III. o. t.)

III. megoldás:

\begin{matrix} tg (45^{\circ} + \frac{α}{2}) = tg \frac{90^{\circ} + α}{2} = \sqrt[]{\frac{1 - cos (90^{\circ} + α)}{1 + cos (90^{\circ} - α)}} = \sqrt[]{\frac{1 + sin α}{1 - sin α}} . \end{matrix}

Természetesen itt is ki kell zárni az

α = \frac{π}{2} \pm 2 k π (k = 0,1,2, ...)

értékeket és a gyök előjelét kellőképpen venni.

Quittner Pál (Bp., I., Petőfi g. III. o. t.)