Kezdőlap


Feladat:	562. matematika feladat	Korcsoport: 18-	Nehézségi fok: átlagos
Megoldó(k):	Deseő Zoltán , Szendrei István
Füzet:	1954/március, 84 - 86. oldal		PDF \| MathML
Témakör(ök):	Szinusztétel alkalmazása, Szélsőérték-feladatok differenciálszámítás nélkül, Síkgeometriai szerkesztések, Feladat
Hivatkozás(ok):	Feladatok: 1953/október: 562. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás: A betűzést az 1. ábra mutatja.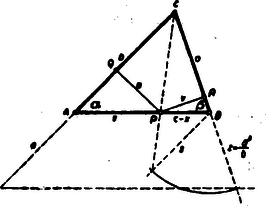

1. ábra

A P = x

, akkor

B P = c - x

, és a két merőleges

u = x sin α

v = (c - x) sin β

.
Tehát az

\begin{matrix} u^{2} + v^{2} = x^{2} sin^{2} α + {(c - x)}^{2} sin^{2} β = x^{2} (sin^{2} α + sin^{2} β) - 2 c x sin^{2} β + c^{2} sin^{2} β \end{matrix}

másodfokú függvény minimumát keressük.
Ismeretes, hogy az

y = a x^{2} + b x + c

függvény szélső értékét az

x = - \frac{b}{a}

helyen veszi fel, és e szélső érték minimum, ha

a > 0

.
Tehát jelen esetben ‐ mivel

sin^{2} α + sin^{2} β > 0

‐ minimum van az

\begin{matrix} x = \frac{c sin^{2} β}{sin^{2} α + sin^{2} β} \end{matrix}

helyen, amikor

\begin{matrix} c - x = \frac{c sin^{2} α}{sin^{2} α + sin^{2} β}, \end{matrix}

és így a sinustétel felhasználásával

\begin{matrix} A P : P B = x : (c - x) = sin^{2} β : sin^{2} α = b^{2} : a^{2} . \end{matrix}

Deseő Zoltán (Bp. X., I. László g. IV. o. t.)

Megjegyzés: A kiszámított arány alapján a

P

pont könnyen meg is szerkeszthető. Pl.

\begin{matrix} b^{2} : a^{2} = b : \frac{a^{2}}{b} = b : z, ahol b : a = a : z . \end{matrix}

z

szakasz tehát negyedik arányosként nyerhető. A szerkesztés az 1. ábráról leolvasható.

II. megoldás: Számítás nélkül tisztán geometriai meggondolásokkal is megszerkeszthető a

P

pont.
Vegyünk fel az

A B

oldalán egy tetszőleges

P_{x}

pontot. A

P_{x}

-ből bocsátott merőlegesek talppontjai legyenek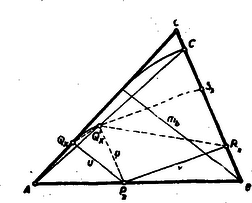

Q_{x}

és

R_{x}

(2. ábra).

2. ábra

P_{x} Q_{x} = u

szakaszt forgassuk el

P_{x}

körül a

P_{x} Q'_{x}

helyzetbe, ahol

P_{x} Q'_{x} ⊥ P_{x} R_{x}

.
Ha

P_{x}

végigfut az

A B

oldalon, akkor a

P_{x} Q_{x} Q'_{x}

egyenlő szárú háromszögek mind hasonlóak és perspektív helyzetűek az

A

centrumra nézve, vagyis a

Q'_{x}

pontok mértani helye az

A Q'_{x}

egyenes, amely a

B C

oldalt a

C'

pontban metszi, ahol

B C'

nyilván nem egyéb, mint a

B

-ből kiinduló

m_{b}

magasság elforgatása

P \equiv B

körül. Pythagoras tétele alapján

u^{2} + v^{2} = Q'_{x} R_{x}^{2}

Q'_{x} R_{x}

pedig a

P_{x} Q'_{x} S_{x} R_{x}

téglalap átlója, amely téglalap az

A B C' ▵

-be van írva oly módon, hogy az

R_{x} S_{x}

oldalának hordozója a háromszög

B C'

oldala.
Problémánk most már így fogalmazható: Az

A B C' ▵

-be írt téglalapok körül (amelyeknek egyik oldala a

B C'

oldal egy szakaszát képezik), melyiknek az átlója a legkisebb?
Hogy ezt meghatározzuk, toljuk el az

A

csúcspontot a

B C'

oldallal párhuzamosan egy tetszőleges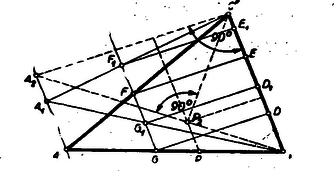

A_{1}

-be (3. ábra).

3. ábra

A B C' ▵

-be írt

D E F G

téglalap akkor eltolódik az

A_{1} C B ▵

-be írt

D_{1} E_{1} F_{1} G_{1}

téglalapba, amely egybevágó az előbbi téglalappal, mert

G_{1} F_{1} : B C' = A_{1} G_{1} : A_{1} B = A G : A B = G F : B C'

, és így

\begin{matrix} G_{1} F_{1} = G F . \end{matrix}

Ha az

A

pontot az

A_{2}

pontba toljuk, ahol

A_{2} C' ⊥ C' B

-re, akkor problémánk így hangzik: A

B C' A_{2}

derékszögű háromszögbe írt téglalapok közül, amelyeknek egyik csúcspontja a

C'

pont, melyiknek átlója minimális? Az

A_{2} B

átfogón lévő

P_{2}

téglalapcsúcspontnak a

C'

csúcsponttól való távolsága a téglalap egyik átlója, amely nyilván akkor minimális, ha

C' P_{2} ⊥ A_{2} B

.
A szerkesztés menete tehát: Megszerkesztjük a

B C

oldalon a

C'

pontot

B C' = m_{b}

alapján (2. ábra). A

C'

pontban merőlegest emelünk a

B C'

oldalra és rámérjük a

C' A_{2} = m_{a}

távolságot (3. ábra).

C'

-ből merőlegest bocsátunk az

A_{2} B

átfogóra, amelynek talppontja

P_{2}

. A

P_{2}

-n át

B C'

-vel rajzolt párhuzamos metszi ki az

A B

oldalból a keresett

P

pontot.

Szendrei István (Kunszentmiklós, Damjanich g. III. o. t.)

Megjegyzés: Könnyen meggyőződhetünk, hogy az így megszerkesztett

P

pont megfelel az I. megoldásban nyert

P

pontnak. Ugyanis az

A_{2} C' B

derékszögű háromszögben (3. ábra), ismert tétel alapján

\begin{matrix} A_{2} C'^{2} = m_{a}^{2} = A_{2} B \cdot A_{2} P_{2} \\ B C'^{2} = m_{b}^{2} = A_{2} B \cdot P_{2} B . \end{matrix}

Tehát

\begin{matrix} \frac{m_{a}^{2}}{m_{b}^{2}} = \frac{A_{2} P_{2}}{P_{2} B} = \frac{A P}{P B} . \end{matrix}

A területképlet alapján azonban

\frac{m_{a}}{m_{b}} = \frac{b}{a}

, és így

\frac{A P}{P B} = \frac{b^{2}}{a^{2}}

, ami egyezik az I. megoldásban nyert eredménnyel.