Kezdőlap


Feladat:	559. matematika feladat	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Forgó Gábor és Imre , Péntek László
Füzet:	1954/március, 81 - 82. oldal		PDF \| MathML
Témakör(ök):	Terület, felszín, Szögfüggvények, síkgeometriai számítások, Feladat
Hivatkozás(ok):	Feladatok: 1953/október: 559. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás: A betűzést az ábra mutatja.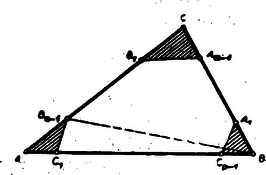

Ha az

A B C ▵

-ből lemetszett

A B_{n - 1} C_{1} ▵

B C_{p - 1} A_{1} ▵

, és

C A_{m - 1} B_{1} ▵

(az ábrában sraffozott) háromszögek területeit rendre

t_{A}

t_{B}

ill.

t_{C}

-vel jelöljük, akkor

\begin{matrix} t_{A} = \frac{1}{2} \cdot \frac{b}{n} \cdot \frac{c}{p} sin α, t_{B} = \frac{1}{2} \cdot \frac{a}{m} \cdot \frac{c}{p} sin β, és t_{C} = \frac{1}{2} \cdot \frac{a}{m} \cdot \frac{b}{n} sin γ . \end{matrix}

Tehát

\begin{matrix} t = T - (t_{A} + t_{B} + t_{C}) = T - (\frac{b c sin α}{2 n p} + \frac{a c sin β}{2 m p} + \frac{a b sin γ}{2 m n}) . \end{matrix}

\begin{matrix} T = \frac{b c sin α}{2} = \frac{a c sin β}{2} = \frac{a b sin γ}{2}, \end{matrix}

és így

\begin{matrix} t = T - (\frac{T}{n p} + \frac{T}{m p} + \frac{T}{m n}) = T (1 - \frac{m + n + p}{m n p}) . \end{matrix}

Péntek László (Kunszentmiklós, Damjanich g. IV. o. t.)

II. megoldás: Az

A B B_{n - 1} ▵

területe

\frac{T}{n}

, mert az

A B

oldala közös az

A B C ▵

A B

oldalával, az ezen közös oldalhoz tartozó magasság pedig

A B C ▵

magasságának az

n

-ed része. Hasonló meggondolással az

A C_{1} B_{n - 1}

területe az

A B B_{n - 1} ▵

területének

p

-edrésze. Tehát

t_{A} = \frac{T}{n p}

. Teljesen ugyanígy látható be, hogy

t_{B} = \frac{T}{m p}

, és

t_{C} = \frac{T}{m n} =

stb., mint az I. megoldásban.

Forgó Gábor és Imre (Bp. V., Eötvös g. II. o. t.)

Megjegyzés: Miután az

m > 2

n > 2

p > 2

feltételeket sehol sem használtuk fel, azért a megmaradt idom területére nyert képlet

m \geq 2

n \geq 2

p \geq 2

esetekben is érvényes, csakhogy ez esetben a megmaradt idom hatszög, ötszög, négyszög vagy háromszög aszerint, amint az egyenlőségi jel

0

1

2

, ill.

3

esetben érvényes.