Kezdőlap


Feladat:	558. matematika feladat	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Csernyák László , Kardos József , Ladoméri Erzsébet
Füzet:	1954/március, 80. oldal		PDF \| MathML
Témakör(ök):	Síkgeometriai számítások trigonometria nélkül körökben, Középpontos és egyéb hasonlósági transzformációk, Húrnégyszögek, Derékszögű háromszögek geometriája, Feladat
Hivatkozás(ok):	Feladatok: 1953/október: 558. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás: Az $A P$ egyenesre mérjük fel a $P C' = P C$ távolságot (1. ábra).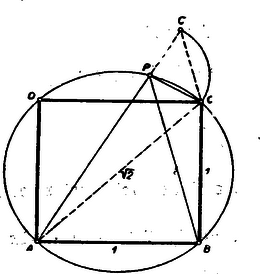

1. ábra

\begin{matrix} A C C' ▵ \sim B C P ▵, \end{matrix}

mert

A ∢ = B ∢

, mint közös íven nyugvó kerületi szögek, és

P ∢ = C' ∢ = 45^{\circ}

. (Előbbi, mint negyedkörön nyugvó kerületi szög, utóbbi, mint egyenlő szárú derékszögű háromszög egyik hegyes szöge, lévén

A P C ∢ = 90^{\circ}

Thales-tétele alapján.)
Tehát ‐ a négyzetoldalt egységnek tekintve ‐

\begin{matrix} A C' : \sqrt[]{2} = B P : 1, \end{matrix}

amiből

\begin{matrix} A C' = A P + P C' = A P + C P = \sqrt[]{2} \cdot B P . \end{matrix}

Ladoméri Erzsébet (Bp. I., Szilágyi Erzsébet lg. IV. o. t.)

II. megoldás: A betűzést a 2. ábra mutatja.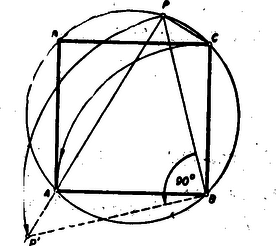

2. ábra

Forgassuk el a

B C P ▵

-et a

B

pont körül

90^{\circ}

-kal az órajárással ellentétes irányban, akkor a

C

pont

A

-ba, a

P

pont pedig

P'

-be kerül. Mivel a Thales-tétel értelmében

C P ⊥ A P

, azért az elforgatás után

A P'

A P

egyenesbe kerül. Tehát

P B B'

egyenlő szárú derékszögű háromszög, melynek átfogója

P P' = P A + A P'

és így Pythagoras tétele szerint

\begin{matrix} P A + A P' = P A + C P = \sqrt[]{2} \cdot B P . \end{matrix}

Kardos József (Miskolc, Földes Ferenc g. IV. o. t.)

III. megoldás: Az

A B C P

húrnégyszögre (1. ábra) alkalmazva a Ptolemaeus-tételt, mely szerint bármely húrnégyszögben az átlók szorzata egyenlő a szemközti oldalak szorzatainak összegével:

\begin{matrix} \sqrt[]{2} \cdot B P = 1 \cdot A P + 1 \cdot C P = A P + C P . \end{matrix}

Csernyák László (Kaposvár, Táncsics g. IV. o. t.)