Kezdőlap


Feladat:	553. matematika feladat	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Szendrei István
Füzet:	1954/március, 73 - 74. oldal		PDF \| MathML
Témakör(ök):	Szögfelező egyenes, Háromszögek szerkesztése, Feladat
Hivatkozás(ok):	Feladatok: 1953/szeptember: 553. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Képzeljük a feladatot megoldottnak. A betűzést az 1. ábra mutatja.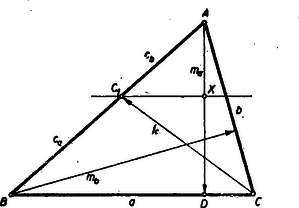

1. ábra

Ismeretes, hogy

f_{c}

c

oldalt olyan

A C_{1} = c_{b}

és

B C_{1} = c_{a}

részekre osztja, melyekre nézve

\begin{matrix} c_{a} : c_{b} = a : b . \end{matrix}

Másrészt a területképlet alapján

\begin{matrix} a : b = m_{b} : m_{a}, \end{matrix}

tehát

\begin{matrix} c_{a} : c_{b} = m_{b} : m_{a} . \end{matrix}

C_{1}

ponton át az

a

oldallal húzott párhuzamos az

m_{a} = A D

magasságot

A X

és

X D

részekre osztja, amelyeknek aránya

\begin{matrix} A X : X D = c_{b} : c_{a} = m_{a} : m_{b} . \end{matrix}

Eszerint a szerkesztés menete: Megrajzoljuk az

a

oldal hordozóját és annak egy tetszőleges

D'

pontjában emelt merőlegesre felmérjük

D' A' = m_{a}

távolságot (2. ábra), melyet

X'

által az

A' X' : X' D' = m_{a} : m_{b}

arányban osztunk.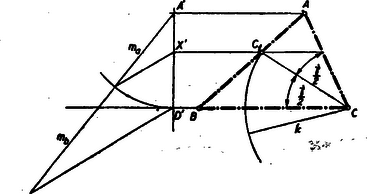

2. ábra

A'

és

X'

pontokon át az

a

oldal hordozójával húzott párhuzamosak lesznek a keresett

A

ill.

C_{1}

pontok mértani helyei. Az

a

hordozónak egy tetszőleges

C

pontjából, mint középpontból, rajzolt

f_{c}

sugarú kör metszi ki a megfelelő mértani helyből a

C_{1}

pontot (a másik metszéspont a most nyert háromszög tükörképét szolgáltatja). A keletkezett

\frac{γ}{2}

szöget a

C C_{1}

másik oldalára másolva, megkapjuk a

C A = b

oldalt.

A C_{1}

metszése az

a

hordozójával adja meg a

B

csúcspontot.

Szendrei István (Kunszentmiklós, Damjanich g. III. o. t.)