Kezdőlap


Feladat:	552. matematika feladat	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Dornbach Alajos , Lábos Elemér , Marik Miklós , Rozsondai Zoltán , Tringer Margit
Füzet:	1954/február, 57 - 58. oldal		PDF \| MathML
Témakör(ök):	Trigonometria, Trigonometrikus egyenletek, Feladat
Hivatkozás(ok):	Feladatok: 1953/szeptember: 552. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás: Ismeretes, hogy $tgα=\sqrt[]{\frac{1 - cos 2 α}{1 + cos 2 α}}$ tehát,

\begin{matrix} tg15^{\circ}=\sqrt[]{\frac{1 - cos 30^{\circ}}{1 + cos 30^{\circ}}}=\frac{\sqrt[]{1 - \frac{\sqrt[]{3}}{2}}}{\sqrt[]{1 + \frac{\sqrt[]{3}}{2}}}=\frac{1 - \frac{\sqrt[]{3}}{2}}{\sqrt[]{1 - \frac{3}{4}}}=\frac{1 - \frac{\sqrt[]{3}}{2}}{\frac{1}{2}}=2-\sqrt[]{3}. \end{matrix}

Teljesen hasonlóan (vagy

cotg 15^{\circ} = \frac{1}{tg 15^{\circ}}

alapján)

\begin{matrix} cotg15^{\circ}=2+\sqrt[]{3}, \end{matrix}

és így

\begin{matrix} tg15^{\circ}+cotg 15^{\circ} =2- \sqrt[]{3} +2+ \sqrt[]{3} =4. \end{matrix}

Marik Miklós (Bp., I., Fürst S. g. IV. o. t.)

II. megoldás:

15^{\circ}

-ot

60^{\circ} - 45^{\circ}

(vagy

45^{\circ} - 30^{\circ}

) alakban írva és alkalmazva a

tg (α - β) = \frac{tg α - tg β}{1 + tg α tg β}

képletet.

\begin{matrix} tg (60^{\circ} - 45^{\circ}) = \frac{tg 60^{\circ} - tg 45^{\circ}}{1 + tg 60^{\circ} tg 45^{\circ}} = \frac{\sqrt[]{3} - 1}{1 + \sqrt[]{3}}, \end{matrix}

és így

\begin{matrix} tg 15^{\circ} + cotg 15^{\circ} = \frac{\sqrt[]{3} - 1}{1 + \sqrt[]{3}} + \frac{1 + \sqrt[]{3}}{\sqrt[]{3} - 1} = \frac{{(\sqrt[]{3} - 1)}^{2} + {(\sqrt[]{3} + 1)}^{2}}{3 - 1} = \frac{8}{2} = 4. \end{matrix}

Dornbach Alajos (Kecskemét, Piarista g. IV. o. t.)

III. megoldás:

\begin{matrix} tg15^{\circ}+cotg 15^{\circ} = \frac{sin 15^{\circ}}{cos 15^{\circ}} + \frac{cos 15^{\circ}}{sin 15^{\circ}} + \frac{{sin}^{2} 15^{\circ} + {cos}^{2} 15^{\circ}}{sin 15^{\circ} cos 15^{\circ}} = \frac{1}{\frac{1}{2} sin 30^{\circ}} = \frac{1}{\frac{1}{4}} =4. \end{matrix}

Tringer Margit (Kaposvár, Munkácsy Mihály lg. IV. o. t.)

Trigonometriai összefüggések ismerete nélkül, csak pusztán a szögfüggvények értelmezését használva fel, is bebizonyíthatjuk tételünket, amint azt az alábbi két megoldás mutatja.

IV. megoldás: Tekintsük a

60^{\circ}

30^{\circ}

-os derékszögű háromszöget, melynek oldalai (a rövidebb befogóval, mint távolságegységgel mérve) tudvalevőleg

1

\sqrt[]{3}

2

(1. 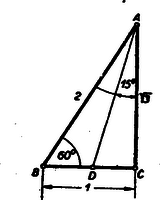ábra).

1. ábra

30^{\circ}

-os szög felezője messe a szemközti egységnyi befogót

D

-ben. Ismeretes, hogy

\begin{matrix} C D : (1 - C D) = \sqrt[]{3} : \sqrt[]{2}, \end{matrix}

amiből

\begin{matrix} C D = \frac{\sqrt[]{3}}{2 + \sqrt[]{3}} . \end{matrix}

Tehát

\begin{matrix} tg15^{\circ}+cotg 15^{\circ} = & \frac{C D}{A C} + \frac{A C}{C D} = \frac{1}{2 + \sqrt[]{3}} + 2 + \sqrt[]{3} = \frac{2 - \sqrt[]{3}}{4 - 3} + 2 + \sqrt[]{3} = 4. \end{matrix}

Razsondai Zoltán (Bp., VIII., Apáczai Csere g. IV. o. t.)

V. megoldás: Rajzoljunk derékszögű háromszöget

15^{\circ}

és

75^{\circ}

-os szögekkel (2. ábra).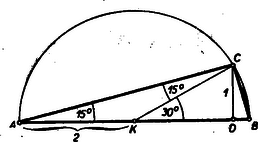

2. ábra

Legyen

K

a köré írt kör középpontja és

D

az átfogóhoz tartozó magasság talppontja.

K C = K A

miatt az

A K C Δ

egyenlőszárú és így a

C K D ∢

, mint külső szög,

30^{\circ}

. Ha a

C D

magasságot egységnek tekintjük, akkor

A K = K C = \frac{1}{sin 30^{\circ}} = 2

, és így

A B = A K + K B = 2 + 2 = 4

.
A

B C D Δ

-ben

tg 15^{\circ} = D B,

A D C Δ

-ben

cotg 15^{\circ} = A D,

és így

\begin{matrix} cotg 15^{\circ} + tg 15^{\circ} = A D + D B = A B = 4. \end{matrix}

Lábos Elemér (Sátoraljaújhely, Kossuth g. III. o. t.)