Kezdőlap


Feladat:	546. matematika feladat	Korcsoport: 18-	Nehézségi fok: nehéz
Megoldó(k):	Almási Z. , Bártfai P. , Beke Éva és Mária , Beke Gy. , Beretvás T. , Biczó G. , Boros P. , Csáki E. , Csanády M. , Csiszár Imre , Csonka P. , Damjanovich S. , Deseő Z. , Eördögh L. , Farkas F. , Gaál I. , Gergely J. , Goldstein R. , Grätzer Gy. , Gutay L. , Gyapjas F. , Hammer E. , Holbok S. , Horváth J. , Horváth Matild , Kántor S. , Klafaszky E. , Kovács László , Lábos E. , Lackner Györgyi , Marik M. , Papp Z. , Pasitka B. , Pátkai Gy. , Peák I. , Rácz M. , Rédly E. , Reichlin V. , Rockenbauer Magda , Sóti F. , Theisz P. , Tóber E. , Tomor B. , Varga Gy. , Vigassy J. , Zawadowski Alfréd , Zsombok Z.
Füzet:	1954/február, 49 - 51. oldal		PDF \| MathML
Témakör(ök):	Szabályos testek, Szélsőérték-feladatok differenciálszámítás nélkül, Szögfüggvények, síkgeometriai számítások, Feladat
Hivatkozás(ok):	Feladatok: 1953/május: 546. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

1. A betűzést az 1. ábra mutatja.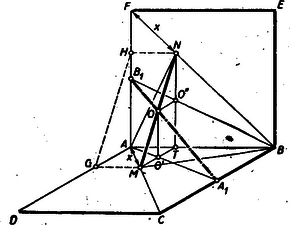

1. ábra

Legyen

M G ⊥ A D

és

N H ⊥ A F

, akkor

A G M

és

F H N

egyenlőszárú derékszögű háromszögek, amelyeknek átfogója

(x)

egyenlő. Tehát

\begin{matrix} A G M_{Δ} ≃ F H N_{Δ}, \end{matrix}

és így

x

-töl függetlenül mindig

\begin{matrix} M G = N H, \end{matrix}

vagyis

M N ∥ G H

. Ebből viszont következik, mivel

G H

állandóan az

A D F

síkban mozog, hogy

M N

állandóan párhuzamos az

A D F

síkkal. (Egy egyenes párhuzamos egy síkkal, ha egy a síkban fekvő egyenessel párhuzamos.)
Mivel

A B ⊥

A D F

síkra (mert e síknak két különböző irányú egyenesére

A D

- és

A F

-re merőleges), azért az

A D F

síkkal párhuzamos

M N

is állandóan merőleges

A B

-re. Az

M N

-en átmenő

A B

-re merőleges sík messe az

A B

-t a

T

pontban. Tehát

M T ⊥ A B

és

N T ⊥ A B

M N

távolság

O

felezőpontjának merőleges vetülete az

A B C D

síkon szükségképpen

M T

felezőpontja

O'

, és

O

merőleges vetülete az

A B E F

négyzetlapra

O''

felezi az

N T

távolságot. (

O O'

ill.

O O''

M T N

derékszögű háromszög középvonalai.) Tehát, ha

x

változik

0

-tól

a \sqrt[]{2}

-ig, az

O

felezőpont leír a térben egy olyan mértani helyet, amelynek merőleges vetülete az

A B C D

négyzetlapon az

O'

pont által befutott

A A_{1}

súlyvonala az

A B C_{Δ}

-nek, míg az

A B E F

síkon levő

O''

vetület leírja a

B B_{1}

súlyvonalát a

B A F_{Δ}

-nek. Ebből következik, hogy

O

pontok mértani helye a

B_{1} A_{1}

távolság, ahol

B_{1}

A F

négyzetoldal,

A_{1}

B C

négyzetoldal felezőpontja.
2. Pythagoras tételének felhasználásával

\begin{matrix} M N^{2} = M T^{2} + N T^{2} = {(\frac{A M}{\sqrt[]{2}})}^{2} + {(\frac{B N}{\sqrt[]{2}})}^{2} = {(\frac{x}{\sqrt[]{2}})}^{2} + {(\frac{a \sqrt[]{2} - x}{\sqrt[]{2}})}^{2} = \\ = \frac{x^{2}}{2} + \frac{2 a^{2} - 2 a x \sqrt[]{2} + x^{2}}{2} = x^{2} - a \sqrt[]{2} x + a^{2} . \end{matrix}

Ennek a függvénynek ábrája egy parabolaív a

0 \leq x \leq a \sqrt[]{2}

intervallumban. E parabolaív végpontjai:

(0, a^{2})

és

(α \sqrt[]{2}, a^{2})

pontok.

{M N}^{2}

így is írható: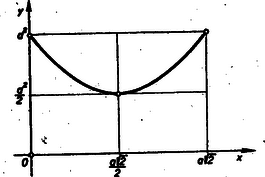

\begin{matrix} M N^{2} = {(x - \frac{a \sqrt[]{2}}{2})}^{2} + \frac{α^{2}}{2}, \end{matrix}

amiből kitűnik, hogy

{M N}^{2}

, és vele együtt

M N

értéke minimális, ha a sohasem negatív első tag

0

, vagyis, ha

\begin{matrix} x = \frac{α \sqrt[]{2}}{2}, mikor is {M N}^{2} = \frac{α^{2}}{2}, azaz M N = \frac{α \sqrt[]{2}}{2} . \end{matrix}

Tehát a parabola főtengelye az

x = \frac{α \sqrt[]{2}}{2}

egyenes, és csúcspontja az

(\frac{α \sqrt[]{2}}{2}, \frac{α^{2}}{2})

pont (2. ábra).

2. ábra

3. Mint láttuk,

M N

minimális, ha

x = \frac{a \sqrt[]{2}}{2}

, vagyis

M

és

N

négyzetközép-pontok, és

M N

minimális értéke

\frac{a \sqrt[]{2}}{2}

. Tehát ebben az esetben az

A M N

és a

B N M

háromszögek egyenlőoldalúak és így kimondhatjuk: ha

M N

minimális, akkor

A M N ∢ = α = 60^{\circ}

, és

B N M ∢ = β = 60^{\circ}

.
4. Mivel

T A = T M

T B = T N

, azért az

\begin{matrix} A T N_{Δ} ≃ M T N_{Δ} ≃ M T B_{Δ}, \end{matrix}

mert mindhárom háromszög derékszögű és befogóik egyenlők. Ebből következik az átfogók egyenlősége, vagyis az

M N A_{Δ}

és az

N M B_{Δ}

egyenlőszárú,

A M

, ill.

B N

alappal. Tehát

\begin{matrix} cos α = \frac{A M}{2 M N} = \frac{x}{2 \sqrt[]{x^{2} - a x \sqrt[]{2} + a^{2}}}, \\ és & cos β = \frac{B N}{2 M N} = \frac{a \sqrt[]{2} - x}{2 \sqrt[]{x^{2} - a x \sqrt[]{2} + a^{2}}} . \end{matrix}

Ebből kitűnik, hogy az

α = β = 90^{\circ}

feltevés arra vezetne, hogy

x

és

a \sqrt[]{2} - x

egyidejűleg

0

volna, ami nyilván lehetetlen, tehát tényleg

M N

nem lehet egyszerre mindkét átlóra merőleges.
5.

x = \frac{a}{2}

esetén

\begin{matrix} cos α = \frac{a}{4 \sqrt[]{\frac{a^{2}}{4} - \frac{a^{2} \sqrt[]{2}}{2} + a^{2}}} = \frac{1}{\sqrt[]{4 - 8 \sqrt[]{2} + 16}} = \frac{1}{2 \sqrt[]{5 - 2 \sqrt[]{2}}} = \frac{1}{2 \sqrt[]{3, 172}}, \end{matrix}

amiből

\begin{matrix} lgcosα=9,5305-10, \end{matrix}

és így

\begin{matrix} α = 70^{\circ} 10' . \end{matrix}

Csiszár Imre (Bp., I., Petőfi g. I. o. t.)