Feladat:	544. matematika feladat	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Bártfai P. ,  Beke Gy. ,  Beretvás T. ,  Biczó G. ,  Csáki E. ,  Csiszár I. ,  Damjanovich S. ,  Deseő Z. ,  Eördögh L. ,  Farkas F. ,  Gaál I. ,  Gergely P. ,  Goldstein R. ,  Grätzer Gy. ,  Gyapjas F. ,  Hammer E. ,  Kántor S. ,  Klafszky E. ,  Kohl Katalin ,  Kovács László ,  Lábos E. ,  Lackner Györgyi ,  Marik M. ,  Mohos B. ,  Papp Z. ,  Pátkai Gy. ,  Péntek L. ,  Quittner P. ,  Roboz Ágnes ,  Rockenbauer Magda ,  Schmidt E. ,  Sóti F. ,  Szabados J. ,  Theisz P. ,  Tomor B. ,  Tóth Ágota ,  Vigassy J. ,  Zawadowski Alfréd ,  Zsombok Z.
Füzet:	1954/január, 24 - 26. oldal		PDF  |  MathML
Témakör(ök):	Hossz, kerület, Terület, felszín, Síkgeometriai szerkesztések, Szögfüggvények, síkgeometriai számítások, Feladat
Hivatkozás(ok):	Feladatok: 1953/május: 544. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.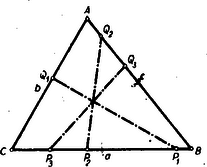   1. ábra   Képzeljük a feladatot megoldottnak pl. az 1. ábrában $P_1{Q}_1$. A $C{P}_1$ távolságot $x$-szel, a $C{Q}_1$ távolságot $y$-nal jelölve, a feladat értelmében $\begin{array}{c}{\displaystyle x+y=s\mathrm{,}}\end{array}$ (1) ahol $s$ a háromszög fél kerülete, és $\begin{array}{c}{\displaystyle \frac{xy\text{sin}\gamma }{2}=\frac{1}{2}\cdot \frac{ab\text{sin}\gamma }{2}\mathrm{,}}\end{array}$ vagyis (mivel $\text{sin}\gamma \ne 0$) $\begin{array}{c}{\displaystyle xy=\frac{ab}{2}\mathrm{.}}\end{array}$ (2) Tehát a feladat most már abból áll, hogy szerkesszünk olyan $x$, $y$ távolságokat, amelyeknek összege $s$ és mértani középarányosa megegyezik $a$ és $\frac{b}{2}$ vagy $b$ és $\frac{a}{2}$ mértani középarányosával.   A szerkesztés menete: Megszerkesztjük $b$ és $\frac{a}{2}$ mértani középarányosát: $\sqrt[]{\fra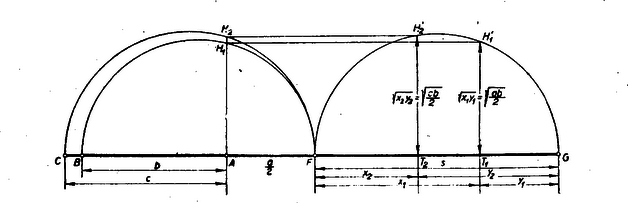c{ab}{c}}=A{H}_1$-et (2. ábra).     2. ábra   Rajzolunk egy $FG=s$ átmérőjű félkört, és húzzunk az átmérővel párhuzamos egyenest, melynek távolsága az átmérőtől $A{H}_1$. Ez a párhuzamos metszi ki a félkörből a $H{\text{'}}_1$ pontot, amelynek vetülete az átmérőn ($T_1$) osztja fel az $s$ átmérőt a keresett $x$ és $y$ részekre. $($A 2. ábrában $\sqrt[]{x_1{y}_1}=H{\text{'}}_1{T}_1=A{H}_1=\sqrt[]{\frac{ab}{2}})$. A megoldhatóság feltételei: (1) és (2)-ből $x$ és $y$-t kiszámítva, nyerjük hogy $\begin{array}{c}{\displaystyle x\left(s-x\right)=\frac{ab}{2}\mathrm{,}\text{vagyis}{x}^2-sx+\frac{ab}{2}=\mathrm{0,}}\end{array}$ amiből $\begin{array}{c}{\displaystyle x_1=y_2=\frac{s+\sqrt[]{s^2-2ab}}{2}\text{és}{x}_2=y_1=\frac{s-\sqrt[]{s^2-2ab}}{2}}\end{array}$ Ahhoz, hogy a feladat az $a$ és $b\left(a>b\right)$ oldalakon megoldható legyen, szükséges és elégséges, hogy a gyökök valósak legyenek és azonkívül a nagyobbik gyök rámérhető legyen a nagyobbik oldalra, a kisebbik gyök pedig a kisebbik oldalra. Elsősorban szükséges tehát, hogy a diszkrimináns ne legyen negatív. Tehát $s^2\ge 2ab$, vagyis $\begin{array}{c}{\displaystyle 4s^2={\left(2s\right)}^2={\left(a+b+c\right)}^2\ge 8ab\mathrm{.}}\end{array}$ (3) Továbbá teljesülnie kell, hogy $\begin{array}{c}{\displaystyle \frac{s}{2}+\frac{\sqrt[]{s^2-2ab}}{2}\le a\mathrm{,}}\end{array}$ (4) és $\begin{array}{c}{\displaystyle \frac{s}{2}-\frac{\sqrt[]{s^2-2ab}}{2}\le b\mathrm{.}}\end{array}$ (5) 1. Bebizonyítjuk, hogy $a>c>b$ esetén e feltételek mindig teljesülnek. (3) teljesül, mert ez esetben a baloldal akkor a legkisebb, ha $c$ a legkisebb, vagyis $c=b$, de $\begin{array}{c}{\displaystyle {\left(a+2b\right)}^2=a^2+4ab+4b^2=a^2-4ab+4b^2+8ab=8ab+{\left(a-2b\right)}^2\ge 8ab\mathrm{,}}\end{array}$ ami nyilván igaz. (4) így írható: $\begin{array}{c}{\displaystyle \sqrt[]{s^2-2ab}\le 2a-s\mathrm{.}}\end{array}$ Mivel $a$ nem a legkisebb oldal, azért a jobboldal pozitív és így négyzetre emelve $\begin{array}{c}{\displaystyle s^2-2ab\le 4a^2-4as+s^2\mathrm{,}}\end{array}$ amiből $\begin{array}{c}{\displaystyle c\le a\mathrm{,}}\end{array}$ ami feltétel szerint igaz, vagyis (4) teljesül. (5) is teljesül, mert ha $b>\frac{s}{2}$, akkor (5) nyilvánvaló, ha pedig $b<\frac{s}{2}$ akkor (5) így írható: $\begin{array}{c}{\displaystyle \frac{\sqrt[]{s^2-2ab}}{2}\ge \frac{s}{2}-b\mathrm{,}}\end{array}$ ahol a jobboldal pozitív, és négyzetre emelés után nyerjük, hogy $\begin{array}{c}{\displaystyle c\ge b\mathrm{,}}\end{array}$ ami mindenképpen igaz. Viszont $\begin{array}{c}{\displaystyle \frac{s}{2}+\frac{\sqrt[]{s^2-2ab}}{2}\le b}\end{array}$ (6) nem teljesül, mert ha $b<\frac{s}{2}$, akkor (6) nem teljesülése nyilvánvaló, ha pedig $b\ge \frac{s}{2}$, akkor (6) így is írható $\begin{array}{c}{\displaystyle \sqrt[]{s^2-2ab}<2b-s\mathrm{,}}\end{array}$ ahol a jobboldal pozitív, és négyzetre emelés után nyerjük $\begin{array}{c}{\displaystyle c\le b\mathrm{,}}\end{array}$ ami ellentmond a feltevésnek. Tehát a legnagyobb és legkisebb oldalon mindig van $\text{<span style="font-style: italic;">1</span>}$ és csakis $\text{<span style="font-style: italic;">1</span>}$ megoldás: a két gyök ilyenkor mindig valós, és a nagyobbik gyök rámérhető a nagyobbik oldalra (és csakis oda) a kisebbik gyök pedig rámérhető a kisebbik oldalra. (Az 1. ábrán $P_1{Q}_1\cdot C{P}_1=x_1$, $C{Q}_1=y_1$). 2. Az előbbiekben láttuk, hogy $a>b$ feltétel mellett (4) csak úgy teljesülhet, ha $c\le a$, ami azt jelenti, hogy az $a$ és $b$ oldalon, csak úgy lehet megoldás, ha $a$-nál nagyobb oldala nincs a háromszögnek, más szóval: a két legkisebb oldalon soha sincs megoldás. 3. $a>b>c$ esetén is lehet az $a$, $b$, azaz a két legnagyobb oldalon megoldás, ha a (3), (4) és (5) alatti feltételek teljesülnek, de ez esetben ‐ mint azt az 1. pontban láttuk ‐ (6) is teljesül, vagyis a nagyobbik gyök a kisebbik oldalra is rámérhető. Tehát lehet a két legnagyobb oldalon 2 megoldás. (Az 1. ábrán $P_2{Q}_2$ és $P_3{Q}_3$. $B{P}_2=B{Q}_3=x_2$, $B{P}_3=B{Q}_2=y_2$). E két megoldásban a háromszögrészek mindig egybevágóak, de a négyszögrészek nem.   Egyenlő oldalú háromszög esetén ($2s=3a$) a gyökök $a$ és $\frac{a}{2}$, vagyis a 3 szimmetria-tengely oldja meg a feladatot. Egyenlő szárú háromszög esetén (alap $\lessgtr$ szár) szimmetrikus megoldások lépnek fel; ezeknek taglalását az olvasóra bízzuk.