Kezdőlap


Feladat:	521. matematika feladat	Korcsoport: 18-	Nehézségi fok: nehéz
Megoldó(k):	Almási L. , Avvakumovits O. , Bába Á. , Babos K. , Balla G. , Bártfai P. , Beke Éva és Mária , Beretvás T. , Biczó G. , Borbély J. , Bujdosó A. , Csáki E. , Csanády M. , Cserni A. , Csiszár I. , Csonka J. , Csonka P. , Dezsényi E. , Eöllös P. , Ferencz F. , Gaál I. , Gergely J. , Gergely P. , Hoffmann S. , Holbok S. , Horváth J. , Horváth Károly , Horváth Matild , Huszár k. , Káfony A. , Kántor S. , Kerényi Gy. , Kéri J. , Kollár L. , Kovács L. , Kulcsár Zsuzsa , Lábos E. , Lévai Mária , Makai I. , Marik M. , Márkus T. , Mészáros F. , Mohos B. , Morva A. , Muzslay L. , Orbán K. , Pál E. , Pasitka B. , Peák I. , Quittner P. , Radda Gy. , Rédly E. , Réthy B. , Rockenbauer Magda , Rozsondai Z. , S. Nagy S. , Sóti F. , Szabados J. , Szabó D. , Szász L. , Szentmártoni Irén , Szuromi L. , Tahy P. , Theisz P. , Tilesch F. , Tomka I. , Tomor B. , Varga E. , Varga György (Baja) , Vass G. , Zawadowski Alfréd , Zsombok Z.
Füzet:	1953/november, 102 - 104. oldal		PDF \| MathML
Témakör(ök):	Szabályos sokszög alapú gúlák, Négyszög alapú gúlák, Derékszögű háromszögek geometriája, Mértani sorozat, Szöveges feladatok, Szögfüggvények, síkgeometriai számítások, Feladat
Hivatkozás(ok):	Feladatok: 1953/február: 521. matematika feladat

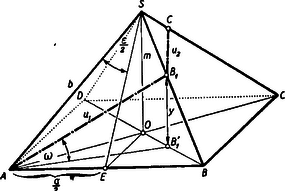
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás: A betűzést az ábra mutatja Számítsuk ki először az $A_{1}$ pontig megtett $u$ utat, amely a következő négy szakaszból tevődik össze; $A B_{1} = u$ , $B_{1} C_{1} = u_{2}$ , $C_{1} D_{1} = u_{3}$ , és $D_{1} A_{1} = u_{4}$ .

Ha a gúla oldalélét

b

-vel és az

S

csúcspontnál lévő élszöget

ε

-nal jelöljük. akkor az

A B_{1} S

derékszögű háromszögből

\begin{matrix} u_{1} = b sin ε, és S B_{1} = b cos ε . \end{matrix}

Hasonlóképpen a

B_{1} C_{1} S

derékszögű háromszögből

\begin{matrix} u_{2} = S B_{1} sin ε = b cos ε \cdot sin ε = u_{1} cos ε . \end{matrix}

B_{1}

C_{1}

D_{1}

pontokon áthaladó, az alaplappal párhuzamos (nívó-) síkok olyan részgúlákat metszenek le az eredeti piramisból, amelyek mind hasonlóak az eredeti gúlához. E hasonlóság alapján kimondhatjuk, hogy a

4

szakasz emelkedési szöge egyenlő, és továbbá

u_{3} = u_{2} cos ε

és

u_{4} = u_{3}

, vagyis a

4

útszakasz mértani sort alkot, amelynek első tagja

u_{1} = b sin ε

, és hányadosa

cos ε

. Tehát

\begin{matrix} u = u_{1} + u_{2} + u_{3} + u_{4} = b sin ε \frac{1 - cos^{4} ε}{1 - cos ε} = b sin ε (1 + cos ε) (1 + cos^{2} ε) . \end{matrix}

(1)

Mivel

A O = \frac{a \sqrt[]{2}}{2}

, vagyis

A O^{2} = \frac{a^{2}}{2}

, azért a piramis oldaléle

\begin{matrix} S A = b = \sqrt[]{m^{2} + A O^{2}} = \sqrt[]{140^{2} + \frac{231^{2}}{2}} = 215, 1. \end{matrix}

A E S

derékszögű háromszögből

sin \frac{ε}{2} = \frac{a}{2 b} = \frac{231}{430, 2}

, amiből

\begin{matrix} \frac{ε}{2} = 32^{\circ} 28', ε = 64^{\circ} 56' . \end{matrix}

Ezen értékeket (I)-be helyettesítve:

\begin{matrix} u = 215, 1 \cdot sin 64^{\circ} 56' \cdot 1, 424 \cdot 1, 180. \end{matrix}

Az iskolai, 4-jegyű lg. táblával számolva az

A_{1}

pontig megtett út

\begin{matrix} u \approx 327, 4 méter . \end{matrix}

A_{1}

pont keresett magasságát

x

-szel, a

B_{1}

pont

B_{1} B'_{1}

magasságát

y

-nal jelölve

\begin{matrix} x : u = y : u_{1}, \end{matrix}

(2)

továbbá a

B O S

derékszögű háromszögben

\begin{matrix} y : m = B_{1} B : b, \end{matrix}

(3)

ahol

\begin{matrix} B_{1} B = b - S B_{1} = b - b cos ε = b (1 - cos ε) = 2 b sin^{2} \frac{ε}{2} . \end{matrix}

Tehát (3)-ból

\begin{matrix} y = \frac{m \cdot B_{1} B}{b} = \frac{m \cdot 2 b sin^{2} \frac{ε}{2}}{b} = 2 m sin^{2} \frac{ε}{2}, \end{matrix}

és így (2)-ből

\begin{matrix} x = \frac{u y}{u_{1}} = \frac{u \cdot 2 m sin^{2} \frac{ε}{2}}{b sin ε} = \frac{u \cdot 2 m sin^{2} \frac{ε}{2}}{b \cdot 2 sin \frac{ε}{2} cos \frac{ε}{2}} = \frac{u m sin \frac{ε}{2}}{b cos \frac{ε}{2}} = \frac{u m tg \frac{ε}{2}}{b} = \\ = \frac{327, 4 \cdot 140 \cdot tg 32^{\circ} 28'}{215, 1}, \end{matrix}

ahonnan az

A_{1}

pont keresett magassága

\begin{matrix} x \approx 135, 6 méter . \end{matrix}

Az emelkedés szögét, a

B_{1} A B'_{1} ∢

-et

ω

-val jelölve

\begin{matrix} sin ω = \frac{y}{u_{1}} = \frac{x}{u} = \frac{135, 6}{327, 4}, \end{matrix}

ahonnan

\begin{matrix} ω = 24^{\circ} 28' . \end{matrix}

II. megoldás: A

b

és

ε

kiszámítása után kiszámíthatjuk először az

A_{1}

pont

x

magasságát.
Ugyanis

x : m = A A_{1} : b

, ahol

A A_{1} = b - S A_{1} S B_{1} = b cos ε

S C_{1} = S B_{1} cos ε = b cos^{2} ε

S D_{1} = S C_{1} cos ε = b cos^{3} ε

és

S A_{1} = b cos^{4} ε

.

Tehát

\begin{matrix} x = \frac{m \cdot A A_{1}}{b} = \frac{m (b - b cos^{4} ε)}{b} = m (1 - cos^{4} ε) (\approx 140 \cdot 0, 9678 \approx 135, 7) \end{matrix}

Az I. megoldás szerint

\begin{matrix} u_{1} = b sin ε, és y = 2 m sin^{2} \frac{ε}{2}, \end{matrix}

tehát

\begin{matrix} sin ω = \frac{y}{u_{1}} = \frac{2 m sin^{2} \frac{ε}{2}}{2 b sin \frac{ε}{2} cos \frac{ε}{2}} = \frac{m tg \frac{ε}{2}}{b} (\approx \frac{140 tg 32^{\circ} 28'}{215, 1}), \end{matrix}

ahonnan

\begin{matrix} ω = 24^{\circ} 28' . \end{matrix}

Mivel

sin ω = \frac{x}{u}

, azért

\begin{matrix} u = \frac{x}{sin ω} (\approx \frac{135, 7}{sin 24^{\circ} 28'} = 327, 6) . \end{matrix}