Feladat: 501. matematika feladat Korcsoport: 16-17 Nehézségi fok: átlagos
Megoldó(k):  Almási L. ,  Avvakumovits O. ,  Bagi A. ,  Balázs B. ,  Bártfai Pál ,  Beke Éva és Mária ,  Beke Gyula ,  Békefi E. ,  Beleznay F. ,  Beretvás T. ,  Biczó G. ,  Biró J. ,  Bódás P. ,  Bujdosó A. ,  Csáki E. ,  Csanády M. ,  Cserni A. ,  Csiszár I. ,  Csonka P. ,  Dabasy H. ,  Damjanovich S. ,  Dancs I. ,  Deli P. ,  Deseő Z. ,  Eöllös P. ,  Farkas E. ,  Ferencz F. ,  Fodor P. ,  Főző Éva ,  Gaál I. ,  Gergely J. ,  Gergely P. ,  Grätzer Gy. ,  Gutay L. ,  Gyapjas F. ,  Gyurányi B. ,  Hackl L. ,  Hoffmann S. ,  Holbok S. ,  Horváth J. ,  Huszár K . ,  Kántor S. ,  Keresztély S. ,  Klafszky E. ,  Kollár L. ,  Kontner L. ,  Kovács F. ,  Kovács L. ,  Krakóczki F. ,  Kulcsár Zsuzsa ,  Küttel I. ,  Lábos E. ,  Magyari-Koss M. ,  Makai I. ,  Martinusz I. ,  Mód S. ,  Mohos B. ,  Molnár I. ,  Németh Gy. ,  Németh L. ,  Ott L. ,  Papp Zoltán ,  Péntek L. ,  Pergel J. ,  Quittner P. ,  Rácz M. ,  Rédly E. ,  Reichlin-M. V. ,  Rockenbauer Magda ,  Rozgonyi I. ,  Rozsondai B. ,  Rozsondai Z. ,  Schmidt E. ,  Sélley G. ,  Sohár P. ,  Sóti F. ,  Szabó D. ,  Szabó J. ,  Szentai E. ,  Szuromi L. ,  Tahy P. ,  Theisz P. ,  Tilesch F. ,  Tisovszky J. ,  Tomor B. ,  Uhrin J. ,  Varga J. ,  Vass Gábor ,  Vértes A. ,  Vigassi J. ,  Zawadowski Alfréd ,  Zobor E. 
Füzet: 1953/október, 58 - 60. oldal  PDF  |  MathML 
Témakör(ök): Beírt háromszög, Forgatva nyújtás, Diszkusszió, Háromszögek szerkesztése, Feladat
Hivatkozás(ok):Feladatok: 1952/december: 501. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás: Mivel a D pont megválasztása után az a=BC oldal tetszés szerinti, D ponton átmenő egyenesen lehet, azért a B és C pontok lényegtelenek, annál is inkább, mert ‐ feladatunk szerint ‐ az E és F pontok az AC=b ill. AB=c egyeneseken bárhol lehetnek. Tehát az ABC▵ helyettesíthető az A pontban metsző b és c egyenesekkel és a 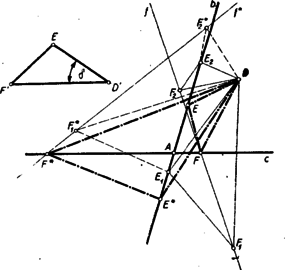D ponttal.
Vegyünk fel a b egyenesen egy tetszőleges E1 pontot és szerkesszünk DE1, mint oldal fölé egy DE1F1 (ill. DE1F1*) háromszöget, amely hasonló a megadott D'E'F'▵-höz (1. ábra).

 
 
1. ábra
 

DF1 (ill. DF1*) felfogható, mint DE1-nek D körüli δ szöggel való elforgatása és ugyanakkor D'F'D'E' arányban való megnyujtása (vagy összehúzása). Mivel ez a transzformáció (l. lapunk 1952. decemberi számában a 135‐136. oldalt) az egyenest egyenesbe viszi át, ezért ha az E pont mozog a b egyenesen, akkor a megfelelő F ill. F* pontok szintén egy-egy egyenest írnak le. Jelöljük ezeket f ill. f*-gal. E két egyenes megszerkesztéséhez elég még egy tetszőleges E2, ponhoz tartozó F2 ill. F2* pontokat megszerkeszteni. F1F2=f, F1*F2*=f*. E két egyenes metszi ki a c egyenesből a keresett F ill. F* pontokat.
Általában tehát 2, különböző körüljárású, háromszög felel meg követelményeinknek. Ha az f és f* közül az egyik párhuzamos c-vel, akkor csak egy megoldás van, viszont ha a két f egyenes közül az egyik egybeesik c-vel, akkor végtelen sok, azonos körüljárású háromszöget és egy ellentétes körüljárású háromszöget kapunk megoldásként.
 

Vass Gábor (Bp. V., Piarista g. III. o. t.)
 

II. megoldás: Fordítsuk meg a feladatot. Írjunk D'E'F'▵ köré az ABC▵-höz hasonló A'B'C' háromszöget, melyet aztán hasonlósági transzformációval átviszünk az adott ABC▵-be.
Képzeljük el, hogy az A'B'C'▵-et megszerkesztettük (2. ábra). Nyilvánvalóan elég az A'-nek helyzetét meghatározni a D'E'F'▵-höz képest. Ha a DA egyenesnek a b és c egyenesekkel bezárt szögét α1 -ill. α2-vel jelöljük, akkor az A'-ből D'E' és D'F'α1 ill. α2 szög alatt látszik.
Tehát az adott D'E'F'▵-höz látókörívek metszéspontjaként (általában 2‐2 látókörív 2 megoldást ad) megszerkesztjük az A' pontot.
 

Bártfai Pál (Bp. I., Petőfi g. II. o. t.)

 
 
2. ábra        3. ábra
 

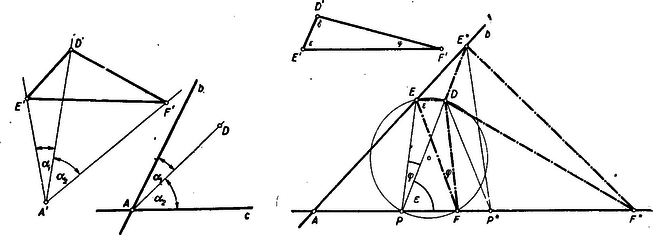III. megoldás: Jelöljük az adott D'E'F' szögeit rendre δ, ε és φ-vel. Természetesen ugyanakkorák a DEF▵ szögei is. Képzeljük a feladatot megoldottnak és írjunk a DEF▵ köré kört, amely a c egyenest, F-en kívül, még a P pontban messe (3. ábra). A kerületi szögek tétele alapján DPF∢=ε és DPE∢=φ. Ennek alapján az adott ε szög segítségével a P (és P*) pont könnyen szerkeszthető. A P (ill. P*) pont birtokában az adott φ szög segítségével megkapjuk a b egyenesen az E (ill. E*) pontot.
 

Papp Zoltán (Sárospatak, Kossuth g. IV. o. t.)