Kezdőlap


Feladat:	499. matematika feladat	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Beke Éva és Mária , Cserni A. , Csomor Z. , Csonka Pál , Deminger K. , Frajka Z. , Füredi F. , Kovács László (Esztergom) , Pap A. , Paveszka J. , Sebők J. , Szabó József (Esztergom)
Füzet:	1953/október, 56 - 57. oldal		PDF \| MathML
Témakör(ök):	Szinusztétel alkalmazása, Koszinusztétel alkalmazása, Mozgással kapcsolatos szöveges feladatok, Feladat
Hivatkozás(ok):	Feladatok: 1952/december: 499. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

A betűzést az ábra mutatja.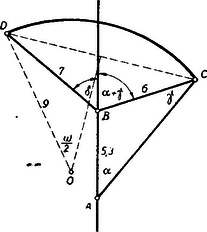

A B C ▵

-ben a sinus-tétel alapján

\begin{matrix} sin γ = \frac{5, 3 sin 38^{\circ} 23'}{6}, amiből γ = 33^{\circ} 15, 5' . \end{matrix}

Ugyanabban a háromszögben, ugyancsak a sinus-tétel felhasználásával

\begin{matrix} A C = \frac{6 sin [180^{\circ} - (α + γ)]}{sin α} = \frac{6 \cdot sin 71^{\circ} 38, 5'}{sin 38^{\circ} 23'} = 9, 17 km . \end{matrix}

B C D ▵

-ben a

D B C ∢ = δ + α + γ = 48^{\circ} 21, 5' + 71^{\circ} 38, 5' = 120^{\circ}

, és így a cosinus-tétel alapján

\begin{matrix} C D^{2} = 6^{2} + 7^{2} - 2 \cdot 6 \cdot 7 cos 120^{\circ} = \\ = 36 + 49 - 84 (- 0, 5) = 36 + 49 + 42 = 127. \end{matrix}

D C

ívhez tartozó középponti szöget

ω

-val jelölve

\begin{matrix} sin \frac{ω}{2} = \frac{\sqrt[]{127}}{2 \cdot 9}, amiből \frac{ω}{2} = 38, 76^{\circ}, ω = 77, 52^{\circ}, \end{matrix}

és így

\begin{matrix} D C = \frac{2 r π ω}{360} = \frac{18 π 77, 52}{360} = \frac{77, 52 π}{20} = 3, 876 π = 12, 18 km . \end{matrix}

A menetidőt megkapjuk, ha az út mértékszámát osztjuk a sebesség mértékszámával.
A szakasz menetideje tehát

\begin{matrix} \frac{9, 17 km}{6 km/óra} + \frac{12, 18 km}{10 km/óra} = 1, 528 óra + 1, 218 óra = 2, 746 óra, \end{matrix}

míg a század menetideje

\begin{matrix} \frac{5, 3 km + 7 km}{5 km/óra} = \frac{12, 3}{5} óra = 2, 46 óra \end{matrix}

A két menetidő különbsége

0, 286 óra \approx 17

perc.
Tehát a századnak 17 perccel később, vagyis 4 óra 12 perckor kell elindulnia.

Csonka Pál (Bp. XI., József Attila g. IV. o. t.)