Kezdőlap


Feladat:	491. matematika feladat	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Ambrus G. , Balatoni F. , Balázs B. , Bártfai Pál , Biczó G. , Bódás P. , Csonka P. , Deseő Z. , Eördögh L. , Gaál I. , Gergely J. , Goldstein R. , Kántor S. , Kelényi Judit , Keresztély S. , Kovács László (Debrecen) , Marik M. , Mohos B. , Molnár I. , Németh Gy. , Ott L. , Pergel József , Reichlin V. , Rockenbauer Magda , Schmidt E. , Sóti F. , Surányi P. , Szabó D. , Szabó József (IV. o.) , Szilárd M. , Tisovszky J. , Tomor B. , Varga J. , Zawadowski Alfréd
Füzet:	1953/szeptember, 21 - 22. oldal		PDF \| MathML
Témakör(ök):	Alakzatba írt kör, Deltoidok, Párhuzamos szelők tétele, Diszkusszió, Négyszögek szerkesztése, Feladat
Hivatkozás(ok):	Feladatok: 1952/november: 491. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás: Képzeljük a feladatot megoldottnak. A betűzést az 1. ábra mutatja.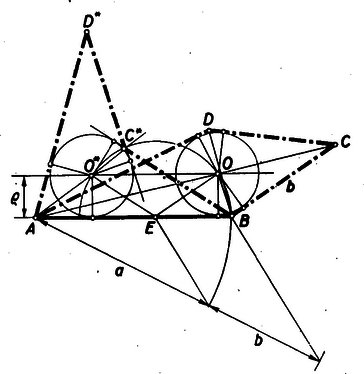

1. ábra

A B C D

deltoidban húzzunk a beirt kör középpontján,

O

-n át párhuzamost a

B C = b

oldallal. Messe ez a párhuzamos az

A B = a

oldalt

E

-ben. A

B O

nyilván szögfelezője az

A B C ∢ = β

szögnek. Tehát

A B O ∢ = O B C ∢ = \frac{β}{2}

de az

O B C ∢

, mint váltószög egyenlő

B O E ∢

-gel és így az

E B O_{▵}

egyenlő szárú:

E B = E O

. Mivel

O E ∥ C B

, azért

A E : E B = A O : O C

. Az ismeretes szögfelezőtétel alapján azonban

A O : O C = a : b

, így tehát

A E : E B = a : b

. Ennek alapján az

E

pont egyszerű arányos osztással megszerkeszthető.
Az

O

pont mértani helye tehát, egyrészt az

A B

-vel húzott párhuzamos egyenes

A B

egyenestől

ϱ

távolságban, másrészt az

E

köré

E B

sugárral rajzolt kör.
Mivel

E B : a = b : (a + b)

, azért

E B = \frac{a b}{a + b}

, és így

2

1

0

megoldás van, aszerint, amint

E B = \frac{a b}{a + b} ⋛ ϱ

.
Ábránkon a 2. megoldás konkáv (homorú) deltoid. Ilyenkor a beírt kör a homorú szöget (

C^{*} ∢ > 180^{\circ}

) bezáró oldalak meghosszabbítását érinti.

Pergel József (Bp. XIX., Landler Jenő g. IV. o. t.)

II. megoldás: A betűzést a 2. ábra mutatja.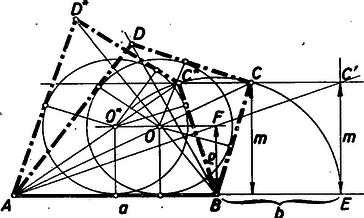

2. ábra

A deltoid területe nyilván egyenlő az

A B C ▵

területének kétszeresével. Utóbbi pedig egyrészt

a ϱ + b ϱ

, másrészt

a m

, ahol

m

a

oldalához tartozó magasság. Tehát

\begin{matrix} a m = (a + b) ϱ, \end{matrix}

vagyis

\begin{matrix} a : ϱ = (a + b) : m, \end{matrix}

és így

m

negyedik arányosként egyszerűen megszerkeszthető.

m

birtokában az adott

a

és

b

oldalakkal az

A B C_{▵}

és így a deltoid szerkesztése is triviális.
A megoldások száma

2

1

0

, aszerint, amint

m = \frac{(a + b) ϱ}{a} ⋚ b

vagyis

ϱ ⋚ \frac{a b}{a + b} .

A szerkesztés menete: Az

A B = a

távolságot megtoldjuk a

B E = b

szakasszal. A

B

pontban

A B

-re emelt merőlegesre felmérjük a

B F = ϱ

távolságot. Az

A F

egyenes metszéspontja az

E

-ben

A E

-re emelt merőlegessel

C'

C' E : (a + b) = ϱ : a

, vagyis

\begin{matrix} C' E = \frac{(a + b)}{a} ϱ = m . \end{matrix}

Bártfai Pál (Bp. I., Petőfi g. II. o. t.)