Kezdőlap


Feladat:	484. matematika feladat	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Bakos K. , Beretvás Tamás , Csonka P. , Deseő Zoltán , Gergely J. , Quittner P. , Sóti F. , Tomor B.
Füzet:	1953/május, 145 - 148. oldal		PDF \| MathML
Témakör(ök):	Kombinatorikai leszámolási problémák, Permutációk, Kombinációk, Feladat
Hivatkozás(ok):	Feladatok: 1952/október: 484. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás: Jelöljük a házaspárokat a következő elemekkel $A a$ , $B b$ , $C c$ , $D d$ . Nem megy az általánosság rovására, ha feltesszük, hogy $A$ mindig megtartja helyét ; akkor a többi $7$ elem $7!$ -féleképpen helyezkedhetik el. De $a$ nem kerülhet $A$ mellé, vagyis $a$ sem második, sem nyolcadik elem nem lehet, vagyis $2 \cdot 6!$ számú csoporttól el kell tekintenünk, Tehát ezen első feltétel figyelembevételével

\begin{matrix} 7! - 2 \cdot 6! \end{matrix}

(1)

számú elhelyezkedés lehetséges.
De

B

sem kerülhet

b

mellé. Azon csoportok száma, amelyekben

B

és

b

szomszédos elemek,

2 \cdot 6!

De ezekből a csoportokból azokat, amelyekben

A

és

a

is egymás mellett vannak, mar tekintetbe vettük. Ilyen csoport (

B

b

és egyúttal

A

a

egymás mellett)

2! 2! = 4

-szer (

A a

B b

;

A a

b B

;

a A

B b

;

a A

b B

) annyi van, mint ahány permutáció képezhető a

C

c

D

d

(B b)

elemekből, ahol

(B b)

egy elemnek számít. Ezeknek a száma tehát

4 \cdot 5!

, és így (1)-ből kivonandó

\begin{matrix} 2 \cdot 6! - 4 \cdot 5! \end{matrix}

(2)

A harmadik feltételt is tekintetbe véve, t. i., hogy

C

sem kerülhet

c

mellé: (1)-ből ismét ki kell vonni

2 \cdot 6!

De (1)-ben már tekintetbe vettük azokat, amelyekben

A

a

és egyúttal

C

c

van egymás mellett, tehát (a fentiek szerint) csak

2 \cdot 6! - 4 \cdot 5!

vonandó ki. De (2)-ben szerepelnek már azok, amelyekben (

A

a

-n kívül)

C

c

is egyúttal

B

b

vannak egymás mellett. Ilyen van

4 \cdot 5! - 2! 2! 2! 4! = 4 \cdot 5! - 8 \cdot 4!

ahol

4!

jelenti a

D

d

(B b)

(C c)

elemekből alkotott permutációk számát.
Tehát (1)-ből még kivonandó

\begin{matrix} (2 \cdot 6! - 4 \cdot 5!) - (4 \cdot 5! - 8 \cdot 4!) . \end{matrix}

A negyedik feltételt is tekintetbe véve, t. i, hogy

D

sem lehet

d

mellett, ‐ az előbbiekhez hasonló meggondolásokkal nyerjük, ‐ hogy (1)-ből még kivonandó

\begin{matrix} (2 \cdot 6! - 4 \cdot 5!) - 2 (4 \cdot 5! - 8 \cdot 4!) + (8 \cdot 4! - 16 \cdot 3!) . \end{matrix}

Ennélfogva végeredményünk:

\begin{matrix} 7! - 2 \cdot 6! - (2 \cdot 6! - 4 \cdot 5!) - (2 \cdot 6! - 4 \cdot 5!) + (4 \cdot 5! - 8 \cdot 4!) - (2 \cdot 6! - 4 \cdot 5!) + \\ + 2 (4 \cdot 5! - 8 \cdot 4!) - (8 \cdot 4! - 16 \cdot 3!) = 7! - 2 \cdot 6! - 2 \cdot 6! + 4 \cdot 5! - 2 \cdot 6! + 4 \cdot 5! + \\ + 4 \cdot 5! - 8 \cdot 4! - 2 \cdot 6! + 4 \cdot 5! + 8 \cdot 5! - 16 \cdot 4! - 8 \cdot 4! + 16 \cdot 3! = 7! - 8 \cdot 6! + 24 \cdot 5! - \\ - 32 \cdot 4! + 16 \cdot 3! = 5040 - 5760 + 2880 - 768 + 96 = 1488. \end{matrix}

II. megoldás: A fenti jelölést megtartva és

A

helyét
megint rögzítve, állapítsuk meg azoknak az elhelyezéseknek számát, amelyekben legalább egy házaspár ül egymás mellett.
a) Négy házaspár hányféleképpen ülhet egymás mellett? Az

(A a)

-t rögzítve, a többi

3

házaspár

3!

‐ féleképpen foglalhat helyet. Ha minden egyes esetben a házastársakat egymás között felcseréljük

{(2!)}^{4} = 16

ülésmódot kapunk. Tehát az összes ülésrendek száma amelyekben mind a

4

házaspár egymás mellett ül

\begin{matrix} 3! 16 = 96. \end{matrix}

(1)

b) Három házaspár egymás mellett, a negyedik szétválasztva. Üljenek egymás mellett az

A

a

;

B

b

;

C

c

házastársak, akkor az

(A a)

(B b)

(C c)

D

d

elemekből ‐ az

(A a)

rögzítése miatt ‐

4!

csoport képezhető. A

3

egymás mellett ülő házaspáron belül a házastársakat felcserélve

{(2!)}^{3} = 8

csoport keletkezik. Tehát az ülésrendek száma

8 \cdot 4!

, de ezekben bennfoglaltaknak az (1) alatti csoportok is, amelyekben

4

házaspár ül egymás mellett. Ezek számát levonva:

8 \cdot 4! - 96

. De

3

házaspárt

4

közül

(\binom{4}{3}) = (\binom{4}{1}) = 4

-félekeppen választhatunk ki és így ezen ülésrendek száma, amelyekben

3

és csakis

3

házaspár ül egymás mellett

\begin{matrix} 4 \cdot (8 \cdot 4! - 96) = 4 (192 - 96) = 4 \cdot 96 = 384, \end{matrix}

(2)

c) Két házaspár egymás mellett, a másik kettő szétválasztva. Tegyük fel, hogy

A

a

és

B

b

ülnek egymás mellett, akkor az

(A a)

(B b)

C

c

D

d

elemekből ‐

(A a)

rögzítése miatt ‐

5!

csoport képezhető. Minden egyes csoportból az egymás mellett ülő házastársakon belül a házastársakat felcserélve

{(2!)}^{2} = 4

csoport keletkezik. Tehát az ülésrendek száma

4 \cdot 5!

, de ezekben bennfoglaltaknak azok a csoportok is, amelyekben

A

a

és

B

b

-n kívül

C

c

, ill.

D

d

is egymás mellett ülnek, továbbá azok a csoportok is, amelyekben mind

C

c

mind

D

d

ülnek egymás mellett. Ilyen csoportok száma ‐ az előbbiek szerint ‐ mind a három esetben

96

. Ezek szerint az olyan ülésrendek száma, amelyekben

A

a

és

B

b

egymás mellett ülnek a másik két házaspár pedig szétválasztva ül

4 \cdot 5! - 3 \cdot 96

. Mivel pedig

2

házaspárt

4

házaspár közül

(\binom{4}{2}) = 6

-féleképpen választhatunk ki, ezért az összes lehetséges elhelyezkedések száma, amelyekben

2

és csakis

2

házaspár ül egymás mellett

\begin{matrix} 6 (4 \cdot 5! - 3 \cdot 96) = 6 (480 - 288) = 6 \cdot 192 = 1152. \end{matrix}

(3)

d) Végül tekintsük azokat az ülésrendeket, amelyekben egy házaspár ül egymás mellett, a többi három szétválasztva. Üljön

A

a

egymás mellett. Az

(A a)

B

b

C

c

D

d

elemektől ‐

(A a)

rögzítése miatt ‐

6!

csoport képezhető, és

A

a

elemek felcserélésével a csoportok száma

2 \cdot 6!

. Ezekben a csoportokban lesznek olyanok, amelyekben

A

a

-n kívül

B

b

;

C

c

és

D

d

házaspárok közül egyik (és csak az egyik) ül egymás mellett. Ilyen van ‐ az előbbiek szerint ‐

3 \cdot 192

. Továbbá foglaltaknak a

2 \cdot 6!

számú csoportban olyanok, amelyekben az utóbbi

3

házaspár közül

2

‐

2

ül egymás mellett. Ilyen van

(\binom{3}{2}) \cdot 96

. Végül lesznek olyan csoportok, amelyikben az

A

a

-n kívül mind a többi

3

házaspár is egymás mellé kerül. Ezen csoportok száma ‐ mind láttuk ‐

96

. Tehát azon csoportok száma, amelyekben csak

A

a

van egymás mellett:

2 \cdot 6! - 3 \cdot 192 - 3 \cdot 96 - 96

, mivel

4

házaspár közül

1

házaspárt

(\binom{4}{1}) = 4

-féleképpen választhatunk ki, azért az összes ülésrendek száma, amelyekben

1

és csakis

1

házaspár ül egymás mellett

\begin{matrix} 4 (2 \cdot 6! - 3 \cdot 192 - 3 \cdot 96 - 96) = 4 (1440 - 576 - 288 - 96) = 4 \cdot 480 = 1920 \end{matrix}

(4)

Tehát a keresett ülésrendek számát megkapjuk, ha az összes lehetséges ülésrend számából kivonjuk az (1), (2), (3) és (4) alatti ülésrendek összegét:

\begin{matrix} 7! - (96 + 384 + 1152 + 1920) - 5040 - 3552 = 1488. \end{matrix}

Deseő Zoltán (Bp., X., I. László g. III. o. t.)

III. megoldás: Jelölés az előbbi. Válasszuk ki a

4

férfi részére az üléshelyek összes lehetséges

11

-féle kombinációját, amint azt az ábra mutatja.

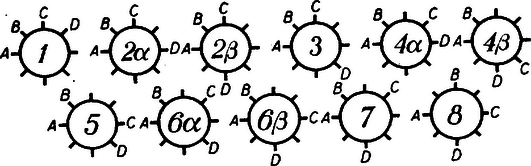Minden egyes esetben helyezzük el (az óramutató járásával megegyező irányban) az

a

b

c

d

feleségeket úgy, hogy az ülésrend feltételeinknek megfeleljen.
1. Ez esetben a nők

4!

számú csoportjából el kell hagyni a

d

-vel kezdődő, ill.

a

-val végződő csoportokat. Ilyen van

2 \cdot 3!

, de akkor a

d

-vel kezdődő és egyszersmind

a

-val végződő

2

csoportot kétszer számítottuk. Tehát a feleségekből alkotható és feltételeinknek megfelelő csoportok száma:

4! - 2 \cdot 3! + 2 = 24 - 12 + 2 = 14

. Ha a férjeket permutáljuk (az elfoglalt üléshelyeket nem változtatva), akkor minden egyes permutációhoz találunk

14

megfelelő női ülésrendet. Tehát az 1. esetben az összes lehetséges ülésrend száma

4! \cdot 14 = 24 \cdot 14 = 336

.
2. Elég az

α

esetet vizsgálni, mert a

β

ennek tükörképe.

C

és

D

közé csak

a

vagy

b

kerülhet. Előbbi esetben a többi

3

feleség

(3! - 2) = 4

-féleképpen helyezkedhetik el

D

és

A

között, míg az utóbbi esetben csak

a c d

a d c

c a d

felel meg feltételeinknek. Tehát

α

esetben

7

α

és

β

esetekben együttvéve

14

-féleképpen ülhetnek a feleségek. Az összes lehetséges ülésrend száma a

2

esetben

4! 14 = 336

.
3. A feleségek megfelelő ülésrendje:

a b c d

a c b d

b a c d

b c a d

d a b c

d a c b

d b a c

d c a b

, vagyis

8

. Összesen

4! 8 = 192

.
4.

α

esetben

B

és

C

közé kerülhet

a

vagy

d

, és mindkét esetben a többi

3

feleség

(3! - 2) = 4

-féleképpen helyezkedhetik el, vagyis

α

esetben

8

féleképpen. Ugyanaz áll a

β

esetben, vagyis a nők összes megfelelő elhelyezkedésének száma

16

. Viszont, ha a férjek összes

24

számú permutációját számba vesszük, akkor csak

12

különböző helyzetet találunk, mert az

α

eset

C D A B

permutációja egyenértékű a

β

eset

A B C D

permutációjával. Tehát az összes ülésrend száma:

\frac{4!}{2} \cdot 16 = 192

.
5. Itt

9

megfelelő ülésrend van a nők számára:

a b c d

a d b c

a d c b

c a b d

c b a d

c d a b

d a b c

d a c b

d b a c

, viszont a férjek

24

permutációjából ismét csak a fele különböző, mert

C D A B

-egyenértékü

A B C D

-vel. Tehát az összes lehetséges ülésrend száma

\frac{4!}{2} \cdot 9 = 108

.
6.

α

esetben

4

ülésrend felel meg:

a b c d

d a b c

d a c b

d b a c

.
Ugyanaz áll a

β

esetre. Tehát az összes ülésrend száma:

4! \cdot 8 = 192

.
7. Itt a nők számára

5

megfelelő ülésrend található:

a d b c

a d c b

d a b c

d a c b

d b a c

. Összesen

4! 5 = 120

.
8. Ez esetben

2

megfelelő ülésrend van:

c d a b

d a b c

. A férjek

24

permutációjából

4

‐

4

egyenértékű (

B C D A

C D A B

D A B C

és

A B C D

) és így csak

6

különböző permutáció jön számításba. Tehát összesen

\frac{24!}{4} \cdot 2 = 12

.
Tehát a keresett ülésrendek száma:

336 + 336 + 192 + 192 + 108 + 192 + 120 + 12 = 1488

Beretvás Tamás (Bp., XIII., Berzsenyi D. g. IV. o. t.)