Kezdőlap


Feladat:	481. matematika feladat	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Ádámfia Károly , Ambrus G. , Argyelán M. , Babos K. , Bagi A. , Balatoni F. , Bali Gy. , Bányai M. , Baráth B. , Bártfai P. , Beretvás T. , Bereznai I. , Biczó G. , Biró J. , Bódás P. , Bogisich F. , Bp. XVI., Corvin Mátyás g. , Búza T. , Böszörményi Nóra , Csáki E. , Csanády M. , Csiszár I. , Csonka P. , Csurgay Á. , Damjanovich S. , Dancs I. , Deseő Z. , Dömölki B. , Edvi Illés Judit , Eichorn József , Eöllős P. , Eördögh L. , Farkas E. , Frivaldszky J. , Gaál I. , Gajzágó V. , Gergely J. , Gergely P. , Gyapjas F. , Gyurányi B. , Hoffmann S. , Holbok S. , Horváth Jenő , Horváth József , Kabók I. , Kántor S. , Kara G. , Kelényi Judith , Kéri J. , Kézdy P. , Klafszky E. , Kocsis J. , Kollányi Veronika , Kontur L. , Koppányi F. , Kovács László (Debrecen) , Kriskó F. , Kristóf F. , Küttel I. , Lábos E. , Magyari-Kossa M. , Marik M. , Marti S. , Martinusz I. , Mercz F. , Miklóssy T. , Mina J. , Misota L. , Mód S. , Mohos B. , Molnár I. , Muzslay L. , Müller L. , Németh Gy. , Ott L. , Paitz J. , Papp Z. , Pasitka B. , Péntek L. , Pergel J. , Pizág J. , Pomogáts B. , Pravecki E. , Quittner P. , Rácz M. , Rédly E. , Reichlin-M. V. , Rockenbauer Magda , Schmidt E. , Schneider J. , Schúder J. , Sohár P. , Sóti F. , Surányi P. , Szabó D. , Szabó József (IV. o.) , Szabó Magdolna , Szarka A. , Tahy P. , Theisz P. , Tilesch F. , Tisovszky J. , Tokaji B. , Tomor B. , Tornyos F. , Uhrin J. , Varga György (IV. o.) , Veidlinger L. , Vida Piroska , Weisz B. , Zawadowski Alfréd , Zobor E.
Füzet:	1953/április, 114 - 116. oldal		PDF \| MathML
Témakör(ök):	Szabályos sokszög alapú gúlák, Négyszög alapú gúlák, Hossz, kerület, Szögfüggvények a térben, Feladat
Hivatkozás(ok):	Feladatok: 1952/október: 481. matematika feladat

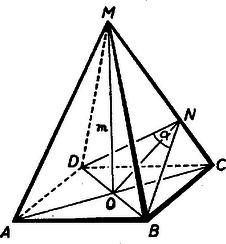
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás: A betűzést azt ábra mutatja.

Legyen a keresett magasság

O M = m

. Mivel a gúla szabályos, azért

B D ⊥ M C

és így lehet a

B D

átlón át síkot fektetni, amely merőleges az

M C

oldalélre. Messe ez a sík az

M C

-t

N

-ben, akkor

B N D_{▵}

egyenlőszárú háromszög, melynek

N

szöge az adott

α

szög.
Az

M N O_{▵} \approx M O C_{▵}

, mert e két háromszög derékszögű és az

M ∢

közös, és így

\begin{matrix} m : O N = M C : O C, \end{matrix}

amiből

\begin{matrix} m = \frac{O N \cdot M C}{O C} . \end{matrix}

(1)

Mivel

\begin{matrix} O B = O D = \frac{a \sqrt[]{2}}{2}, azért O N = \frac{a \sqrt[]{2}}{2} cotg\frac{α}{2}. \end{matrix}

(2)

Pythagoras tétele alapján

\begin{matrix} M C = \sqrt[]{\frac{a^{2}}{2} + m^{2}}, \end{matrix}

(3)

és

\begin{matrix} O C = \frac{a \sqrt[]{2}}{2} . \end{matrix}

(4)

A (2), (3) és (4) alatti értékeket (1)-be helyettesítve

\begin{matrix} m = \sqrt[]{\frac{a^{2}}{2} + m^{2}} \cdot cotg\frac{α}{2}, \end{matrix}

vagyis

\begin{matrix} m^{2} = \frac{a^{2}}{2} {c o t g}^{2}\frac{α}{2}+m^{2} {c o t g}^{2}\frac{α}{2}, \end{matrix}

amiből

\begin{matrix} m = \sqrt[]{\frac{a^{2} {c o t g}^{2}\frac{α}{2}}{2 (1 - {c o t g}^{2}\frac{α}{2})}} = \frac{a}{\sqrt[]{2 {t g}^{2}\frac{α}{2}-2}} . \end{matrix}

(5)

Megjegyzés: Az (5) alatti eredmény jobboldala egyenértékű a következő kifejezésekkel:

\begin{matrix} \frac{a cos \frac{α}{2}}{\sqrt[]{2 cos (180 - α)}} = a \sqrt[]{\frac{1 + cos α}{4 cos (180 - α)}} = \frac{a cos \frac{α}{2}}{\sqrt[]{2 - 4 cos^{2} \frac{α}{2}}} = \frac{α}{2} \sqrt[]{cotg\frac{α}{2}tg(180^{\circ} - α)} \end{matrix}

stb. stb. Ha mindezekbe a kifejezésekbe

α = 120^{\circ}

-ot helyettesítünk, megkapjuk a Rákosi versenypéldában szereplő speciális

m = \frac{a}{2}

értéket.

m

-re csak akkor kapunk valós és véges értéket, ha

90^{\circ} < α

. Az

α < 180^{\circ}

felső határ az

α

értelmezéséből adódik.

Eichorn József (Pécs, Nagy Lajos g. IV. o. t.)

II. megoldás: Tekintsük a két gúlát, amelyeknek közös alapja a

B N D ▵

és magassága

N M

ill.

N C

. E két gúla köbtartalmának összege egyenlő az eredeti gúla köbtartalmának felével, azaz (a közös alap területét

t

-vel jelölve)

\begin{matrix} t \frac{N M}{3} + t \frac{N C}{3} = \frac{a^{2}}{2} \cdot \frac{m}{3}, \end{matrix}

ahonnan

\begin{matrix} t \cdot M C = \frac{a^{2}}{2} \cdot m . \end{matrix}

Tehát

\begin{matrix} m = \frac{2 t \cdot M C}{a^{2}} = \frac{a \sqrt[]{2} \cdot O N \cdot M C}{a^{2}} = \frac{O N \cdot M C \cdot \sqrt[]{2}}{a}, \end{matrix}

ami azonos az I. megoldás (1) alatti összefüggésével.