|
| Feladat: |
480. matematika feladat |
Korcsoport: 16-17 |
Nehézségi fok: átlagos |
| Megoldó(k): |
Ambrus G. , Avvakumovits O. , Babos K. , Bagi A. , Balatoni F. , Balázs B. , Bali Gy. , Baráth B. , Bártfai P. , Beke Éva és Mária , Beleznay F. , Beretvás T. , Bereznai I. , Biczó G. , Biró J. , Bódás P. , Búza T. , Csáki E. , Csernyák L. , Csiszár I. , Csonka P. , Dancs I. , Deseő Z. , Döbrösy K. , Dömölki B. , Eördögh L. , Frajka Z. , Frivaldszky J. , Gaál I. , Gajzágó V. , Gerey F. , Gergely J. , Gergely P. , Gulyás l. , Gutay L. , Gyapjas F. , Gyurányi B. , Györe I. , Hammer E. , Hoffmann S. , Horváth J. , Horváth József , Huszár k. , Ivanyos A. , Kabók I. , Kántor Sándor , Kardou B. , Kéri J. , Kézdy P. , Kiss A. , Klafszky E. , Kollányi Veronika , Kontur L. , Kovács F. , Kovács László (Debrecen) , Kriskó F. , Kristóf T. , Lábos E. , Lackner Györgyi , Lepsényi J. , Magyary-Kossa M. , Marik M. , Marti S. , Mátrai Gy. , Mercz F. , Mina J. , Misota Lajos , Mohos B. , Molnár J. , Molnár T. , Müller L. , Nagy B. , Nagy Lajos , Nagy S. , Németh Gy. , Németh I. , Obermájer M. , Paitz J. , Pál E. , Papp Z. , Pázmándy Gy. , Péntek L. , Pergel J. , Pohlinger l. , Pravecki E. , Quittner P. , Rácz M. , Radda Gy. , Rédly E. , Reichlin-M. V. , Rockenbauer Magda , Sáfrán L. , Schmidt E. , Schmidt Ibolya , Schneider J. , Schúder J. , Sohár P. , Sóti F. , Surányi P. , Szabados L. , Szabó D. , Szabó J. , Szilárd M. , Szlukovényi F. , Telkes Z. , Theisz P. , Tilesch F. , Tisovszky J. , Tóka P. , Tokaji B. , Tomor B. , Tóth Ildikó , Uhrin J. , Varga György (Baja) , Varga Tünde , Vass G. , Weisz B. , Weisz Edit , Zawadowski Alfréd , Zobor E. |
| Füzet: |
1953/április,
112 - 114. oldal |
 PDF | PDF |  MathML MathML |
| Témakör(ök): |
Elsőfokú (és arra visszavezethető) egyenlőtlenség-rendszerek, Háromszögek nevezetes tételei, Alakzatok mértéke, Szinusztétel alkalmazása, Koszinusztétel alkalmazása, Diszkusszió, Feladat |
| Hivatkozás(ok): | Feladatok: 1952/október: 480. matematika feladat |
|
|
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. I. megoldás: Mivel , azért az legnagyobb oldala, és így és
Azt kell bizonyítani, hogy az (1), ill. (2)-ben szereplő oldalakból háromszöget lehet szerkeszteni. Ennek szükséges és elégséges feltétele, hogy a legnagyobb oldal kisebb legyen a másik két oldal összegénél, vagyis
De (3) közvetlenül következik (2) első egyenlőtlenségéből és (4) közvetlenül (1) első részének folyománya.
Ezzel tételünk első részét bebizonyítottuk.
Jelöljük az (1) alatti oldalukból szerkesztett háromszög szögeit rendre , és -vel.
Az eredeti -ből a cosinus tétel alapján | | (5) |
mivel .
Másrészt a megszerkesztett háromszögből ugyancsak a cosinus‐tétel felhasználásával | | (6) |
(5) és (6)-ból következik, hogy | |
amiből | |
és így vagyis
A sinus‐tétel szerint
Mivel | |
azért és közül egyik sem fekszik a legnagyobb oldallal szemben, tehát egyikük sem lehet tompaszög, vagyis és | |
A másik háromszöggel nem kell külön foglalkozni, mert csak és oldalakat, ill. és szögeket kell egymás között felcserélni.
| Kántor Sándor (Debrecen, Ref. g. IV. o. t.) |
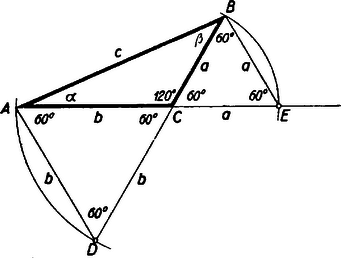
II. megoldás: Állításunkat azzal bizonyíthatjuk, hogy tényleg megszerkesztjük az , , és , , oldalú háromszögeket.
Rajzoljuk meg az adott -et, melyben . (L. ábrát). Hosszabbítsuk meg az és oldalakat -n túl a , illetőleg szakaszokkal. Mivel mellékszöge , azért az és háromszögek nemcsak egyenlő szárúak, hanem egyenlő oldalúak, és így és a keresett háromszögek, melyeknek szögei tehát illetőleg
| Misota Lajos (Pécs, Nagy Lajos g. IV. o. t.) |
|
|
 PDF
PDF