Kezdőlap


Feladat:	478. matematika feladat	Korcsoport: 18-	Nehézségi fok: átlagos
Megoldó(k):	Almási L. , Bártfai P. , Beretvás T. , Biczó G. , Bujdosó A. , Csiszár I. , Csomor J. , Csonka P. , Deseő Z. , Eördögh L. , Gergely J. , Gergely P. , Gutay L. , Gyapjas F. , Holbok S. , Huszár k. , Kántor S. , Klafszky E. , Koppányi F. , Kovács László (Debrecen) , Küttel I. , Németh Gy. , Névtelen , Ott L. , Quittner P. , Rékasi L. , Rockenbauer Magda , Sohár P. , Surányi P. , Szabó József (IV. o.) , Theisz P. , Tokaji B. , Tomor B. , Varga György (Baja) , Zobor E.
Füzet:	1953/április, 109 - 111. oldal		PDF \| MathML
Témakör(ök):	Gyökös függvények, Függvényvizsgálat, Szélsőérték-feladatok differenciálszámítás nélkül, Feladat
Hivatkozás(ok):	Feladatok: 1952/október: 478. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Egyelőre tekintsünk el a konkrét numerikus adatoktól, csak azt tételezzük fel, hogy $a > b$ .
Tárgyalásunkat egyszerűsíthetjük, ha mindjárt az elején a következő megállapításokat tesszük:
1. Görbénk ‐ a négyzetgyök két ellenkező jelű értéke miatt ‐ az $x$ tengelyre nézve szimmetrikus két ágból áll.
2. Görbénk az $y$ tengelyre is tükrös, mert csak $x^{2}$ -es tagok fordulnak elő, és így $y$ értéke $a + x$ helyen ugyanaz, mint a $- x$ helyen.
Elég tehát csak pozitív $x$ és $y$ értékekre szorítkozni. Alakítsuk át az

\begin{matrix} y = + {[\frac{4 a^{2} x^{2} + b^{2} {(x^{2} - 1)}^{2}}{{(x^{2} + 1)}^{2}}]}^{\frac{1}{2}} \end{matrix}

függvényt a következőképpen:

\begin{matrix} y = {[\frac{4 a^{2} x^{2} + b^{2} x^{4} - 2 b^{2} x^{2} + b^{2}}{{(x^{2} + 1)}^{2}}]}^{\frac{1}{2}} = {[\frac{4 a^{2} x^{2} - 4 b^{2} x^{2} + b^{2} {(x^{2} + 1)}^{2}}{{(x^{2} + 1)}^{2}}]}^{\frac{1}{2}} = \\ = {[\frac{4 (a^{2} - b^{2}) x^{2}}{{(x^{2} + 1)}^{2}} + b^{2}]}^{\frac{1}{2}} = {[\frac{4 (a^{2} - b^{2})}{{(\frac{x^{2} + 1}{x})}^{2}} + b^{2}]}^{\frac{1}{2}} \end{matrix}

\begin{matrix} {(\frac{x^{2} + 1}{x})}^{2} = {(x + \frac{1}{x})}^{2} = x^{2} + 2 + \frac{1}{x^{2}} = 4 + x^{2} - 2 + \frac{1}{x^{2}} = 4 + {(x - \frac{1}{x})}^{2}, \end{matrix}

és így függvényünk ilyen alakban írható:

\begin{matrix} y = f (x) = {[\frac{4 (a^{2} - b^{2})}{4 + {(x - \frac{1}{x})}^{2}} + b^{2}]}^{\frac{1}{2}} . \end{matrix}

Ebből az alakból rögtön leolvasható, hogy egyedül a nevező változó, és mivel a feltételünk szerint a számláló mindig pozitív, ezért függvényünknek ott lesz minimuma illetőleg maximuma, ahol a nevező a legnagyobb ill. legkisebb.

a) A nevező a legnagyobb, ha vagy

x

nő minden határon túl, vagy

\frac{1}{x}

nő minden határon túl, vagyis

x

nullává válik. E két esetben

(x = 0, \infty)

tehát a szögletes zárójelben lévő tört 0-vá válik és így

\begin{matrix} y_{{min}_{}^{}} = {[b^{2}]}^{\frac{1}{2}} = b . \end{matrix}

Görbénk tehát az

x = 0

helyen felülről érinti az

y = b

egyenest, és ha

x

minden határon túlnő

(x \to \infty)

akkor a görbénk felülről aszimptotikusan közeledik az

y = b

végérintőhöz (aszimptotához).

b) A nevező a legkisebb, ha az állandóan pozitív

{(x - \frac{1}{x})}^{2} = 0

, vagyis

x = \frac{1}{x}

, azaz

x = 1

(a megállapodásunknak megfelelően csak pozitív értéket véve figyelembe).

Tehát az

x = 1

helyen

f (x)

-nek maximuma van, és

\begin{matrix} y_{{max}_{}^{}} = {[(a^{2} - b^{2}) + b^{2}]}^{\frac{1}{2}} = a \end{matrix}

Görbénk tehát az

x = 1

helyen alulról érinti az

y = a

egyenest.
Tehát, ha

x

változik 0-tól 1-ig, akkor

y

nő

b

-től

a

-ig, és ha

x

nő 1-től minden határon túl, akkor

y

csökken

a

-tól

b

-ig olymódon, hogy mindenkor

\begin{matrix} f (x) = f (\frac{1}{x}), \end{matrix}

amint erről közvetlenül behelyettesítés útján meggyőződhetünk:

\begin{matrix} {(x - \frac{1}{x})}^{2} = {(\frac{1}{x} - x)}^{2} . \end{matrix}

Áttérve most már az

a = 3

b = 2

numerikus adatokra

\begin{matrix} y = f (x) = {[\frac{20}{4 + {(x - \frac{1}{x})}^{2}} + 4]}^{\frac{1}{2}} \end{matrix}

és néhány helyen kiszámítva az

f (x)

értékét, a következő értéktáblázatot nyerjük:

\begin{matrix} x & 0 & 0, 1 & 0, 2 & 0, 4 & 0, 5 & 0, 6 & 0, 8 & 1 \\ \infty & 10 & 5 & 2, 5 & 2 & 1, 67 & 1, 25 \\ y & 2 & 2, 05 & 2, 18 & 2, 53 & 2, 68 & 2, 81 & 2, 96 & 3 \end{matrix}

A teljes görbét az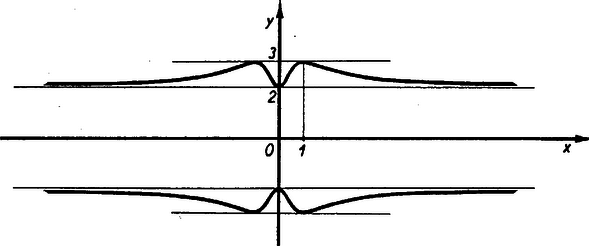

x

és

y

tengelyeken át való tükrözéssel nyerjük. (l. ábrát)

Számos ábra hibája, hogy a szélső értékeknél a görbe nem érinti az

y = \pm 2

és

y = \pm 3

egyeneseket.