Kezdőlap


Feladat:	470. matematika feladat	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Andrási S. , Avvakumovits O. , Balatoni F. , Bárdos A. , Bártfai P. , Bereznai I. , Biczó G. , Borbály J. , Bujdosó A. , Búza T. , Csernyák L. , Darvas I. , Deák Judith , Deseő Z. , Eördögh M. , Fülöp J. , Gyapjas F. , Haász Anna , Hátsági V. , Hoffmann S. , Horváth I. , Huszár k. , Kántor S. , Kiss A. , Klofszky E. , Kollár L. , Kontur L. , Kovács F. , Kovács László (Debrecen) , Kozma Vera , Küttel I. , Kövecs J. , Lackner Györgyi , Marik M. , Marx Klára , Micsei S. , Németh Gy. , Papp Z. , Pergel J. , Rácz M. , Reichlin M. V. , Rockenbauer Magda , Rozgonyi I. , Rusznyák A. , Schmidt Eligius , Schúder J. , Sélley G. , Simon J. , Sohár P. , Sóti F. , Szabó D. , Szilárd M. , Tahy P. , Tilesch F. , Tisovszky J. , Tomor B. , Tornyos F. , Tóth Mária , Vigassy J. , Weisz B. , Zawadowski Alfréd , Zobor E.
Füzet:	1953/március, 75 - 76. oldal		PDF \| MathML
Témakör(ök):	Súlyvonal, Szögfelező egyenes, Síkgeometriai számítások trigonometria nélkül körökben, Háromszögek szerkesztése, Feladat
Hivatkozás(ok):	Feladatok: 1952/szeptember: 470. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás: Képzeljük a feladatot megoldottnak (1. ábra). A betűzést az ábra mutatja.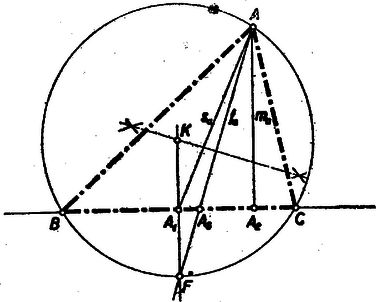

1. ábra

Egészítsük ki ábránkat a háromszög köré írt körrel és messe az

A_{1}

ponton átmenő oldalfelező merőleges azt a

B C

ívet, amelyen nincs rajta az

A

pont,

F

-ben. Mivel a húrfelező merőleges a húrhoz tartozó körívet is felezi, azért a

B F

ív

= F C

ívvel és így a kerületi szögek tétele alapján az

f_{a}

szögfelező meghosszabbítása átmegy az

F

ponton. Ebből viszont az is következik, hogy

A_{3}

mindenkor (hacsak

A_{1}

nem azonos

A_{2}

)

A_{1}

és

A_{2}

között fekszik, vagyis

m_{a} <

< f_{a} < s

. (Ha

A_{1}

azonos

A_{2}

-vel, akkor a háromszög egyenlő szárú

m_{a} = f_{a} = s_{a}

és a feladat határozatlan.)
Eszerint a szerkesztés menete: Felveszünk a

B C = a

oldal hordozó egyenesét és azon az

A_{2}

pontot. Az

A_{2}

-ben az

a

-ra emelt merőlegesre felmérjük az

A_{2} A = m_{a}

távolságot. Az

A

pontból, mint középpontból az

f_{a}

és

s_{a}

szakaszokkal rajzolt körívek metszik ki az

A_{2}

-nek ugyanazon az oldalán, az

A_{3}

és

A_{1}

pontokat. (

A_{3}

pont

f_{a} < s_{a}

miatt

A_{2}

és

A_{1}

között.) Az

A_{1}

-ben

a

-ra emelt merőleges metszéspontja az

A A_{3}

szögfelezővel szolgáltatja az

F

pontot. Az

A F

húrfelező merőleges egyenes metszi ki az

A_{1} F

egyenesből a háromszög köré írt kör középpontját:

K

-t. E pont kerül

K A = K F

sugárral rajzolt kör metszése az

a

oldal hordozójával adja a

B

és

C

csúcspontokat.

Kozma Vera (Bp. V., 1. sz. textilip. techn. II. o. t.)

II. megoldás: Az

A_{1}

és

A_{3}

pontok megszerkesztése után, az

F

pont és a körülírt kör nélkül is, megszerkeszthetjük a

B

és

C

csúcspontokat.
Rajzoljuk meg az

A

csúcsponton át az

f_{a}

-ra merőleges külső szögfelezőt, amely az

a

oldal hordozóját az

A'_{3}

pontban metszi. (2. ábra)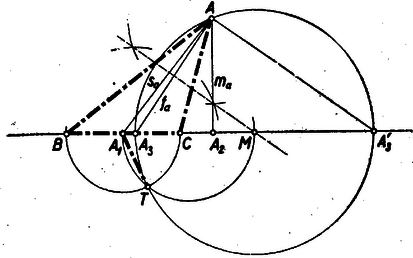

2. ábra

A_{3} A'_{3}

szakasz fölé, mint átmérő fölé rajzolt kör (amely Thales tétele alapján átmegy az

A

ponton), nem egyéb, mint a

B C

oldalhoz tartozó

A

-n átmenő Apollonius-féle kör. Állítjuk, hogy az

A_{1}

pontból ezen körhöz szerkesztett érintő

A_{1} T = A_{1} B = A_{1} C = \frac{a}{2}

.
Bizonyítás: Legyen

A_{1} A_{3} = p

A_{1} A'_{3} = q

, akkor

\begin{matrix} \frac{A_{3} C}{A_{3} B} = \frac{A'_{3} C}{A'_{3} B}, \end{matrix}

vagyis

\begin{matrix} \frac{\frac{a}{2} - p}{\frac{a}{2} + p} = \frac{q - \frac{a}{2}}{q + \frac{a}{2}} . \end{matrix}

A törteket eltávolítva és rendezve

\begin{matrix} 2 a^{2} = 8 p q, \end{matrix}

amiből

\begin{matrix} \frac{a}{2} = \sqrt[]{p q} . \end{matrix}

De az

A_{1}

pontból a körhöz szerkesztett érintő ‐ ismert tétel alapján ‐ mértani középarányos a

p

és

q

metszetek között, vagyis tényleg

A_{1} T = \frac{a}{2}

Schmidt Eligius (Bp. I., Fürst S. g. III. o. t.)