Kezdőlap


Feladat:	468. matematika feladat	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Argyelán M. , Avvakumovits O. , Babos K. , Bagi A. , Baitz T. , Balatoni F. , Balázs B. , Bali Gy. , Bányai M. , Barcza S. , Bárdos A. , Bártfai P. , Beke Éva és Mária , Beretvás T. , Bereznai I. , Biczó G. , Biró J. , Bódás P. , Bogisián F. , Bp. XIII., Berzsenyi g. , Bp. XVI., Corvin Mátyás g. , Bujdosó A. , Búza T. , Csáki E. , Csanády M. , Csiszár I. , Csiszár Imre , Csonka P. , Damjanovich S. , Dancs I. , Debrecen, 3. sz. vegyip. techn. , Deseő Z. , Dohonics L. , Drasny J. , Dudás G. , Dömölki B. , Edvi Illés Judit , Esztergom, I. István g. , Eördögh L. , Fodor A. , Frajka Z. , Frivaldszky J. , Gaál I. , Gaál Ö. , Gerey F. , Gergely A. , Grätzer Gy. , Gutay L. , Gyapjas F. , Gyenes Gy. , Győre I. , Gyurányi B. , Gyurmits F. , Hajas S. , Halász S. , Hegedüs Z. , Hoffmann S. , Horváth J. , Horváth Mária , Huszár k. , Jókai Z. , Kántor S. , Kántor Sándor , Kapitány Gy. , Kelényi Judit , Kéri J. , Kiss A. , Kissik A. , Klofszky E. , Kocsis J. , Kollár L. , Kovács István , Kovács László (Debrecen) , Küttel I. , Köves J. , Lajtai J. , Latzkovits L. , Lepsényi I. , Lipka I. , Magyar K. , Marik M. , Mercz F. , Mód S. , Mohos B. , Molnár I. , Muzslay L. , Nagy B. , Nagy S. , Nagykanizsa, Irányi Dániel g. , Nálint Irma , Németh Gy. , Németh P. , Németh S. , Pálla Gabriella , Pap A. , Papp Z. , Pasitka B. , Pergel J. , Pranecki E. , Pusztai Mária és Ilona , Radda Gy. , Rédly E. , Rékasi L. , Rockenbauer Magda , Rozsondai B. , Rusznyák A. , Sáfrán L. , Savanyó L. , Schmidt E. , Sebők J. , Siklósi P. , Simon J. , Sohár P. , Sóti F. , Surányi P. , Szabó D. , Szabó I. , Szabó József (IV. o.) , Szabó M. , Szabó Magdolna , Szegletes I. , Szeleczki Klára , Tahy P. , Telkes Z. , Tisovszky J. , Tokaj B. , Tomor B. , Tornyos F. , Varga Gy. (IV. o.) , Varga Tünde , Varkas E. , Vida Piroska , Vigassy J. , Weisz B. , Zawadowski Alfréd , Zobor Ervin
Füzet:	1953/március, 72 - 74. oldal		PDF \| MathML
Témakör(ök):	Trigonometriai azonosságok, Szinusztétel alkalmazása, Szögfüggvények, síkgeometriai számítások, Feladat
Hivatkozás(ok):	Feladatok: 1952/szeptember: 468. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás.
Először megnézzük, hogy a jobboldalon álló tört nevezője $x$ milyen értékénél egyenlő zéróval.
Ha az ismeretes

\begin{matrix} tg x = tg 2 \cdot \frac{x}{2} = \frac{2 tg \frac{x}{2}}{1 - {tg}^{2} \frac{x}{2}} \end{matrix}

azonosságban

tg \frac{x}{2}

helyébe

t

-t írunk, akkor

tg x = \frac{2 t}{1 - t^{2}}

és a kérdéses nevező

\begin{matrix} 1 + tg x tg \frac{x}{2} = 1 + \frac{2 t}{1 - t^{2}} \cdot t = 1 + \frac{2 t^{2}}{1 - t^{2}} = \frac{1 + t^{2}}{1 - t^{2}} . \end{matrix}

Ez a kifejezés csak úgy lehet nulla, ha

t^{2} = - 1

, ami lehetetlen.
Eszerint a bizonyítandó azonosságnak mindig van értelme, hacsak a benne előforduló

cos x

tg x

tg \frac{x}{2}

-nek van értelme. Közülük

cos x

mindig értelmezve van,

\begin{matrix} tg x -nek az x = \pm \frac{π}{2}, \pm \frac{3 π}{2} ... -nél \\ tg \frac{x}{2} -nek az x = \pm π, \pm 3 π ... -nél \end{matrix}

nincs értelme.

x

ezen értékeit kizárjuk.
Mivel bizonyítandó azonosságunk nevezője sohasem veszi fel a

0

értékét, ezért egyenlőségünk mindkét oldalát megszorozhatjuk a nevezővel:

\begin{matrix} cos x (1 + tg x tg \frac{x}{2}) = 1, \end{matrix}

azaz

\begin{matrix} cos x + sin x \cdot \frac{sin \frac{x}{2}}{cos \frac{x}{2}} = 1. \end{matrix}

Tekintettel a kizárt értékekre, mindkét oldalt megszorozhatjuk

cos \frac{x}{2}

-vel:

\begin{matrix} cos x \cdot cos \frac{x}{2} + sin x sin \frac{x}{2} = cos \frac{x}{2} \end{matrix}

vagyis

\begin{matrix} cos (x - \frac{x}{2}) = cos \frac{x}{2}, \end{matrix}

ami tényleg azonosság.

Csiszár Imre (Bp. I., Petőfi g. I. o. t.)

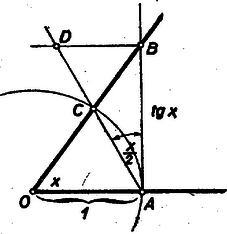
II. megoldás: Állítsuk elő az

O A = 1

sugarú körben az

x

szög tangensét

A B

-t (l. ábrát).

O B

szögszárnak az egységsugarú körrel való metszéspontját

C

-vel jelölve, a

B A C ∢ = \frac{x}{2}

, mint kerületi szög és így az

A C B ∢ = 180^{\circ} - (90^{\circ} - x) - \frac{x}{2} = 90^{\circ} + \frac{x}{2}

.

Az

A B C ▵

-re alkalmazva a sinustételt:

\begin{matrix} \frac{B C}{A B} = \frac{sin \frac{x}{2}}{sin (90^{\circ} + \frac{x}{2})} = \frac{sin \frac{x}{2}}{cos \frac{x}{2}} = tg \frac{x}{2}, \end{matrix}

vagyis

B C = A B tg \frac{x}{2} = tg x tg \frac{x}{2}

,

és így

cos x = \frac{O A}{O B} = \frac{O A}{O C + C B} = \frac{1}{1 + tg x tg \frac{x}{2}}

, ami bizonyítandó volt.

Megjegyzés: Ez a bizonyítás kiterjeszthető a többi szögnegyedekre is.

Zobor Ervin (Nagykanizsa, Irányi D. g. IV. o. t.)

III. megoldás: Emeljünk

B

-ben

A B

-re merőleges egyenest és messe ez az egyenes az

A C

húr meghosszabbítását

D

-ben. Az így keletkezett

C B D ▵

‐ a szögek egyenlősége miatt ‐ hasonló a

C O A

egyenlő szárú háromszöghöz, vagyis

C B = D B = A B \cdot tg \frac{x}{2} = tg x tg \frac{x}{2}

stb. mint a II. megoldásban.