Kezdőlap


Feladat:	456. matematika feladat	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Balázs B. , Bali Gy. , Beke Éva és Mária , Durst E. , Gaál I. , Gyapjas F. , Kántor S. , Kovács L. , Marik M. , Németh László , Pergel J. , Rockenbauer Magda , Rozsondai B. , Schmidt Eligius , Száz K. , Zawadowski Alfréd
Füzet:	1953/január, 25 - 27. oldal		PDF \| MathML
Témakör(ök):	Fizikai jellegű feladatok, Merőleges affinitás, Ellipszis egyenlete, Parabola, mint kúpszelet, Szögfüggvények, síkgeometriai számítások, Hajítások, Feladat
Hivatkozás(ok):	Feladatok: 1952/május: 456. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás: A fizikából ismeretes, hogy a parabolapálya csúcspontjának koordinátái

\begin{matrix} x = \frac{c^{2} sin 2 α}{2 g}, & (1) \\ y = \frac{c^{2} sin^{2} α}{2 g} . & (2) \end{matrix}

A legmagasabb az emelkedés, ha

α = 90^{\circ}

, amikor is

y_{max} = \frac{c^{2}}{2 g}

. Ezen érték helyett az egyszerűség kedvéért

2 m

-et írva, az (1) és (2) alatti egyenletek a következő alakot veszik fel:

\begin{matrix} x = 2 m sin 2 α, & (3) \\ y = 2 m sin^{2} α . & (4) \end{matrix}

A mértani hely egyenletét megkapjuk, ha a tetszőleges értéket felvevő

α

paramétert kiküszöböljük.
Mivel

2 sin^{2} α = 1 - cos 2 α

, azért a (4) alatti egyenlet

\begin{matrix} y = m (1 - cos 2 α) = m - m cos 2 α, \end{matrix}

amiből

\begin{matrix} cos^{2} 2 α = \frac{{(y - m)}^{2}}{m^{2}}, \end{matrix}

(5)

(3)-ból

\begin{matrix} sin^{2} 2 α = \frac{x^{2}}{{(2 m)}^{2}} . \end{matrix}

(6)

(5) és (6)-ot összeadva és az egyenlet két oldalát felcserélve

\begin{matrix} \frac{x^{2}}{{(2 m)}^{2}} + \frac{{(y - m)}^{2}}{m^{2}} = 1. \end{matrix}

Ez egy olyan ellipszis egyenlete, melynek középpontja

K

(0,

m

), nagy tengelye párhuzamos az abszcissza tengellyel és a fél nagy tengely hossza

2 m

, az ordináta tengelyre eső kis tengely fele:

m

. Ezen adatokból az is kitűnik, hogy az ellipszis érinti az origóban az

x

tengelyt. Ebből az ellipszisből a keresett mértani helynek ‐

0^{\circ} \leq α \leq 90^{\circ}

feltétel miatt ‐ csak az

y

tengelytől jobbra eső fél ellipszis felel meg.

m = \frac{c^{2}}{4 g}

, vagyis ha

g

-t állandónak tekintjük, akkor

m

csak a

c

-től függ.

m

változásával az ellipszisek csak nagyságra változnak, egymás között mind hasonlók.

II. megoldás: Legyen

P

(

4 m sin α cos α

2 m sin^{2} α

) a mértani hely egy pontja, ahol

2 m = \frac{c^{2}}{2 g} = y_{max}

. Vizsgáljuk meg azon

P'

pontok geometriai helyét, amelyeket a

P

pontok ordinátáinak megkettőzésével nyerünk. (L. ábrát, amely a betűzést is mutatja.)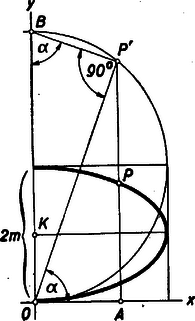

Tehát

P'

koordinátái:

4 m sin α cos α

4 m sin^{2} α

.
Az

O P'

iránytangense=

\frac{4 m sin^{2} α}{4 m sin α cos α} = \frac{sin α}{cos α} = tg α

, vagyis

O P'

x

tengellyel a hajítás szögét zárja be.

P'

-ben az

O P'

-re bocsátott merőleges messe az

y

tengelyt egy

B

pontban. A merőleges szárú szögpárok tétele alapján

P' B O ∢ = α

.
Pythagoras‐tétele alapján

\begin{matrix} O P' = \sqrt[]{A P'^{2} + A O^{2}} & = \sqrt[]{16 m^{2} sin^{4} α + 16 m^{2} sin^{2} α cos^{2} α} = \\ = \sqrt[]{16 m^{2} sin^{2} α (sin^{2} α + cos^{2} α)} = 4 m sin α, \end{matrix}

és így

O B = \frac{O P'}{sin α} = 4 m

α

-tól független állandó.
A

P'

pontok mértani helye tehát az

O B = 4 m

fölé rajzolt Thales‐körnek az

y

tengelytől jobbra eső fele.
E kör egyenlete

\begin{matrix} x^{2} + {(y - 2 m)}^{2} = {(2 m)}^{2} . \end{matrix}

P

pontok keresett mértani helye pedig e félkör pontjaihoz tartozó ordináták felezőpontjai.
E felező pontok mértani helye tehát

\begin{matrix} x^{2} + {(2 y - 2 m)}^{2} = {(2 m)}^{2}, \end{matrix}

vagyis

\begin{matrix} \frac{x^{2}}{{(2 m)}^{2}} + \frac{{(y - m)}^{2}}{m^{2}} = 1, ahol x \geq 0. \end{matrix}

Ez a fél ellipszis a félkörnek az

y

tengely irányában

λ = \frac{1}{2}

arányban való

≫

összenyomása

≪

által keletkezett. (Lásd ált. gimnáziumok IV. oszt. tankönyvében: Függvény transzformációk 4. pontja, 43‐44. oldal.)

Schmidt Eligius (Bp. I., Fürst S. g. II. o. t.)