Kezdőlap


Feladat:	453. matematika feladat	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Bajnógel J. , Balatoni F. , Bali Gy. , Csaba L. , Csáki E. , Gergely A. , Gutay L. , Hartmann E. , Horváth J. , Horváth K. , Kántor S.. , Klofszky E. , Lipka I. , Marik M. , Németh László , Rockenbauer Magda , Rozsondai B. , Schmidt E. , Szász K. , Szathury Éva , Tilesch F. , Tomor B. , Viski Mária , Zatykó L. , Zawadowski Alfréd
Füzet:	1953/január, 20 - 22. oldal		PDF \| MathML
Témakör(ök):	Hossz, kerület, Alakzatok mértéke, Négyszögek geometriája, Koszinusztétel alkalmazása, Síkgeometriai számítások trigonometriával, Feladat
Hivatkozás(ok):	Feladatok: 1952/május: 453. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

A betűzést az ábra mutatja.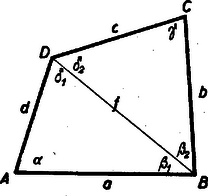

B D = f

átlót a cosinus-tétellel egyrészt az

A B D_{▵}

-ből, másrészt a

B C D_{▵}

-ből kifejezve:

\begin{matrix} f = a^{2} + d^{2} - 2 a d cos α = b^{2} + c^{2} - 2 b c cos γ, \end{matrix}

amiből

\begin{matrix} cos γ = \frac{b^{2} + c^{2} - a^{2} - d^{2} + 2 a d cos α}{2 b c} . \end{matrix}

(1)

Az oldalakat rendre egy

x

arányossági tényezővel kifejezve:

\begin{matrix} a = 9 x, b = 8 x, c = 7 x, d = 6 x . \end{matrix}

Ezen értékeket (1)-be helyettesítve

\begin{matrix} cos γ = \frac{64 x^{2} + 49 x^{2} - 81 x^{2} - 36 x^{2} + 108 x^{2} cos α}{112 x^{2}} = \frac{27 cos α - 1}{28} = \frac{7, 086}{28}, \end{matrix}

amiből

\begin{matrix} γ = 75^{\circ} 22' . \end{matrix}

(

γ

másik értéke:

284^{\circ} 38'

jelen esetben hurkolt négyszöghöz vezet.)
A négyszög kétszeres területe:

\begin{matrix} a d sin α + b c sin γ = 450, \end{matrix}

vagyis

\begin{matrix} 54 x^{2} sin α + 56 x^{2} sin γ = 450, \end{matrix}

amiből

\begin{matrix} x^{2} = \frac{450}{54 sin 72^{\circ} 36' + 56 sin 75^{\circ} 22'} = \frac{450}{105, 72}, \end{matrix}

és így

\begin{matrix} x = 2, 063. \end{matrix}

Ennélfogva

\begin{matrix} a = 18, 567 cm, b = 16, 504 cm, c = 14, 441 cm  és d = 12, 378 cm . \end{matrix}

A még hiányzó két szög kiszámítását megoldóink túlnyomó része ‐ tangens‐tétel hiányában ‐ úgy végezték, hogy az

a

d

és

α

adatokból a kellemetlen cosinus-tétellel (főleg akkor kellemetlen, ha nem ismerjük a logaritmus használatra alkalmas alakját) kiszámították az

f

átlót és ezután a sinus-tétel kétszeri alkalmazásával a

β_{1}

és

β_{2}

szögeket.
A tangens-tétellel az

f

átló fáradságos kiszámítását megtakaríthatjuk és közvetlenül kiszámíthatjuk a

β_{1}

és

δ_{1}

valamint

β_{2}

és

δ_{2}

szögeket. A tangens-tétel a sinus-tételből rövid úton levezethető:

\begin{matrix} a : b = sin α : sin β, \end{matrix}

amiből

\begin{matrix} (a + b) : (a - b) = (sin α + sin β) : (sin α - sin β), \end{matrix}

vagyis

\begin{matrix} \frac{a + b}{a - b} = \frac{2 sin \frac{α + β}{2} cos \frac{α - β}{2}}{2 cos \frac{α + β}{2} sin \frac{α - β}{2}} = tg \frac{α + β}{2} \cdot cotg \frac{α - β}{2} = \frac{tg \frac{α + β}{2}}{tg \frac{α - β}{2}} . \end{matrix}

(2)

Ezzel már meg is van a tangens‐tétel.
Mivel

\frac{α + β}{2} = \frac{180^{\circ} - γ}{2} = 90^{\circ} - \frac{γ}{2} és tg (90 - \frac{γ}{2}) = cotg \frac{γ}{2}

,

azért (2)-ből

\begin{matrix} tg \frac{α - β}{2} = \frac{(a - b) cotg \frac{γ}{2}}{a + b}, \end{matrix}

(3)

A (3) alatti képletet az

A B D_{▵}

-re alkalmazva

\begin{matrix} tg \frac{δ_{1} - β_{1}}{2} = \frac{(a - d) cotg \frac{α}{2}}{a + d} = \frac{6, 189 cotg 36^{\circ} 18'}{30, 945}, \end{matrix}

amiből

\begin{matrix} \frac{δ_{1} - β_{1}}{2} = 15^{\circ} 15', \end{matrix}

vagyis

\begin{matrix} δ_{1} - β_{1} = 30^{\circ} 30' . \end{matrix}

(4)

Másrészt

\begin{matrix} δ_{1} + β_{1} = 180^{\circ} - α = 107^{\circ} 24', \end{matrix}

(5)

és így (4) és (5)-ből

\begin{matrix} δ_{1} = 68^{\circ} 57' és β_{1} = 38^{\circ} 27' . \end{matrix}

Hasonlóképpen a

B C D_{▵}

-ből

\begin{matrix} tg \frac{δ_{2} - β_{2}}{2} = \frac{(b - c) cotg \frac{γ}{2}}{b + c} = \frac{2, 063 cotg 37^{\circ} 41'}{30, 945}, \end{matrix}

amiből

\begin{matrix} \frac{δ_{2} - β_{2}}{2} = 4^{\circ} 56', \end{matrix}

vagyis

\begin{matrix} δ_{2} - β_{2} = 9^{\circ} 52', \end{matrix}

és mivel

\begin{matrix} δ_{2} + β_{2} = 180^{\circ} - γ = 104^{\circ} 38', \end{matrix}

azért

\begin{matrix} δ_{2} = 57^{\circ} 15' és β_{2} = 47^{\circ} 23' . \end{matrix}

Tehát

\begin{matrix} β = β_{1} + β_{2} = 85^{\circ} 50', \end{matrix}

és

\begin{matrix} δ = δ_{1} + δ_{2} = 126^{\circ} 12' . \end{matrix}

Rockenbauer Magda (Bp. X., I. László g. III.)