Kezdőlap


Feladat:	450. matematika feladat	Korcsoport: 16-17	Nehézségi fok: könnyű
Megoldó(k):	Balaton F. , Bali Gy. , Csaba L. , Csáki E. , Dancs I. , Deseő Z. , Durst I. , Főző Éva , Francsics I. , Fülöp J. , Gaál I. , Grätzer Gy. , Gutay L. , Gyapjas F. , Gyenes Gy. , Hadi I. , Horváth J. , Huszár k. , Kántor S. , Kovács László , Lipka I. , Marik Miklós , Miklós Margit , Mohos B. , Nagy B. , Németh László , Révi F. , Rockenbauer Magda , Schmidt E. , Schmidt I. , Szabó J. , Szabó Magdolna , Tilesch F. , Tomor B. , Vigassy József , Zatykó L. , Zawadowski Alfréd
Füzet:	1953/január, 15 - 17. oldal		PDF \| MathML
Témakör(ök):	Trigonometrikus egyenlőtlenségek, Trigonometriai azonosságok, Feladat
Hivatkozás(ok):	Feladatok: 1952/május: 450. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás: Mivel $α$ hegyesszög, azért egyenlőtlenségünk mindkét oldala pozitív, tehát négyzetre emelhető, vagyis elegendő a következő egyenlőtlenséget igazolni:

\begin{matrix} sin^{2} α + cos^{2} α + 2 sin α cos α \leq 2. \end{matrix}

\begin{matrix} sin^{2} α + cos^{2} α = 1, 2 sin α cos α = sin 2 α \end{matrix}

és így

\begin{matrix} sin 2 α \leq 1, \end{matrix}

ami nyilván igaz. Az egyenlőségi jel akkor érvényes, ha

α = 45^{\circ}

Marik Miklós (Bp. I., Fürst S. g. II. o. t.)

II. megoldás:
Az

α

hegyesszög mindig ilyen alakban írható

\begin{matrix} α = 45^{\circ} \pm β, ahol 0 \leq β < 45^{\circ} . \end{matrix}

Tehát

\begin{matrix} sin α & = sin 45^{\circ} cos β \pm cos 45^{\circ} sin β = \frac{\sqrt[]{2}}{2} (cos β \pm sin β) & (1) \\ cos α & = cos 45^{\circ} cos β \mp sin 45^{\circ} sin β = \frac{\sqrt[]{2}}{2} (cos β \mp sin β) & (2) \end{matrix}

(1) és (2) összege:

\begin{matrix} sin α + cos α = \sqrt[]{2} cos β \end{matrix}

Tehát

sin α + cos α

lehető legnagyobb értéke

\sqrt[]{2}

, midőn

cos β = 1

, vagyis

β = 0^{\circ}

és így

α = 45^{\circ}

Zawadowski Alfréd (Bp. I., Petőfi g. III. o. t.)

III. megoldás: Vegyünk fel egy

A B = 1

szakaszt és rajzoljuk meg azt a körívet, amelynek pontjaiból az

A B

távolság

45^{\circ}

alatt látszik. (1. ábra.)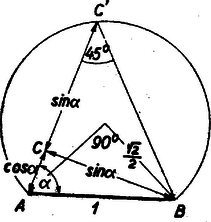

1. ábra

Mivel a középponti szög

90^{\circ}

, azért a látókörív sugara

\frac{\sqrt[]{2}}{2} \cdot A B

fölé

A B C

derékszögű háromszöget szerkesztve, melynek

A

-nál levő szöge tetszőleges

α

, akkor

A C = cos α

és

B C = sin α

. Messe az

A C

befogó meghosszabbítása a látókörívet

C'

pontban, akkor a keletkezett

B C C'

derékszögű háromszög egyenlő szárú, mert

C' ∢ = 45^{\circ}

, vagyis

C C' = C B = sin α

. Tehát

A C' = sin α + cos α

. Ha

α

változik, az

A C'

húr is változik, de mindig kisebb marad az átmérőnél,

\sqrt[]{2}

-nél. A legnagyobb értéket

sin α + cos α = A C'

akkor éri el, ha

A C'

átmérő, vagyis

A C' = \sqrt[]{2}

és ez esetben

α = 45^{\circ}

. (Az 1. ábrából még leolvasható, hogy ha

α

hegyesszög, akkor

A C' = sin α + cos α

minimális értéke 1, midőn

α = 90^{\circ}

Vigassy József (Bp. I., Petőfi g. II. o. t.)

IV. megoldás: Próbáljuk grafikusan megoldani a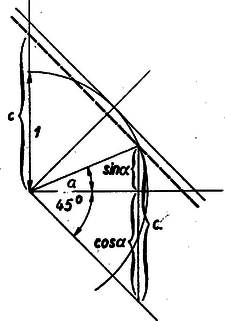

\begin{matrix} sin α + cos α = c \end{matrix}

egyenletet, ahol

c

megadott konstans érték. (2. ábra) A

c

-hez tartozó

α

szöget úgy nyerjük, hogy a

≫

45^{\circ}

-os

≪

szög mozgó szárát önmagával párhuzamosan eltoljuk

c

távolsággal.

2. ábra

Az eltolt egyenes (ábránkon vonalkázva), általában 2 pontban metszi a negyedkört, tehát 2 megoldást kapunk

α

-ra. A

c

-t változónak tekintve,

α

-ra hegyesszögű megoldás a

c

változónak csak bizonyos intervallumában van:

c

legkisebb értéke 1, mikor is

α_{1} = 0^{\circ}

és

α_{2} = 90^{\circ}

és legnagyobb értéke pedig midőn

α_{1} = α_{2} = 45^{\circ}

, vagyis az eltolt egyenes érinti a negyedkört. Ez esetben

c = \sqrt[]{2}

. Tehát ha

α

hegyesszög

\begin{matrix} 1 \leq sin α + cos α \leq \sqrt[]{2} . \end{matrix}

Megjegyzés: Ha elejtjük azt a követelményt, hogy a hegyesszög, akkor ábránkból rögtön látható, hogy

\begin{matrix} - \sqrt[]{2} \leq c \leq \sqrt[]{2} \end{matrix}

esetén van megoldás.

Kovács László (Debrecen, Ref. g. II. o. t.)