| Feladat: | 446. matematika feladat | Korcsoport: 16-17 | Nehézségi fok: nehéz |
| Megoldó(k): | Biczó G. , Csáki E. , Deseő Zoltán , Durst E. , Dömölki Bálint , Kántor S. , Marik Miklós , Németh László , Rockenbauer Magda , Rozsondai B. , Schmidt E. , Szabó J. , Tahy Péter | ||
| Füzet: | 1952/december, 146 - 151. oldal |  PDF | PDF |  MathML MathML |
|
| Témakör(ök): | Sakk, Kombinatorikai leszámolási problémák, Permutációk, Kombinációk, Sakktáblával kapcsolatos feladatok, Feladat | ||
| Hivatkozás(ok): | Feladatok: 1952/április: 446. matematika feladat | ||
|
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. a) I. megoldás: 14 lépés esetén a bástya mindig csak a szomszédos mezőre léphet ‐ jobbra, vízszintes irányban, vagy előre függőleges irányban, mert -től -ig összesen 7‐7 egységlépést kell tennie mindkét irányban. Ha a vízszintes lépést -val és a függőleges lépést -vel jelképezzük; akkor egy tetszőlegesen kiragadott utat például így jelezhetünk: . Tehát minden útnak az elemeknek egy permutációja felel meg és megfordítva: az említett permutációk mindegyikének egy út.
II. megoldás: Minden mezőbe írjuk be az összes arra vezető utak számát elölről kezdve folytatólagosan. Ez utóbbi számot nyilván úgy kapjuk meg, ha összeadjuk abba a két mezőbe írt számot, amely két mezőről az illető mezőre léphettünk. (1. ábra) 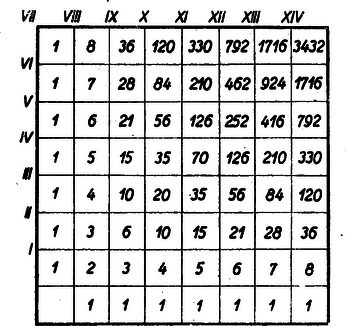 Kiindulás: - és -be 1-et írunk s. i. t. a fenti szabály szerint. Ennek alapján a beírt számok olyan Pascal-féle háromszöget alkotnak, amelynek az mező a csúcsa és melyben az , , , stb. átlók a sorai. A mezőbe tehát a 14. sor 8-ik tagja kerül:
III. megoldás: Az átló egyes mezeire a bástya -ből kiindulva feltételünknek megfelelően , , , , -féleképpen juthat el (L. előbbi megoldást és 1. ábrát.) Minden egyes mezőről a bástya nyilván ugyanannyiféleképpen mehet el -ra, ahányféleképpen eljutott az átló illető mezejére. Tehát az összes lehetséges utak száma Ennek a megoldásnak az az előnye, hogy egyszersmind megadja az átló minden egyes mezejére nézve külön-külön az illető mezőn átvonuló utak számát. Pl. -on út vonul át.
IV. megoldás: Állapítsuk meg egy tetszőleges lépésszámra érvényes képletet, ahol ‐ az értelmezésből kifolyólag ‐ természetes szám, melyre nézve . Először is nyilvánvaló, hogy elég azokat az utakat megszámlálni, amelyekben az első lépés függőleges, mert ezen utaknak az átlóra vonatkozó tükörképei szolgáltatják a vízszintes kezdőlépésű utakat és fordítva. Tehát az összes utak száma: az előbbi kikötés mellett megszámlált utak kétszerese. Mivel az utolsó lépés mindig -ra történik, ezért pl. valamely 12 lépéses út jelölésére elég azt a 11 mezőt megadni, amely mezőkön egy-egy lépés végződik. Valamely tetszőleges 12 lépéses utat pl. a következő 11 lépésvégponttal jelölhetünk a sakktábla mezeinek szokásos jelölését használva: . (2. ábra.) 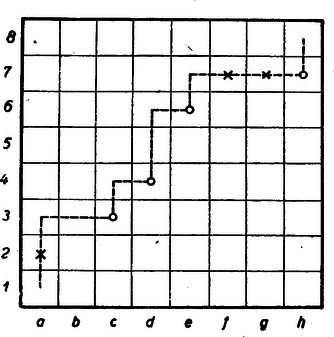 A lépésvégpontok lehetnek olyan pontok, amelyekben irányváltozás történik és olyanok amelyekben nem történik irányváltozás. Ez előbbieket nevezzük töréspontoknak. Ezeknek számát -val jelölve, lépés esetén . Az utóbbiakat nevezzük megállók-nak. Ezeknek számát nyilvánvalóan megkapjuk, ha az lépés-végpontból a töréspontok számát levonjuk: . (Ha , akkor nincs megálló). A fenti példában 8 töréspontot találunk: , , , , , , , és megállót: , és . (Az ábrában fekvő kereszttel jelölve). A töréspontok teljesen meghatározzák az útvonalat (nem az utat, mert az út ismeretéhez még a megállók ismerete is szükséges), sőt elég pl. a vízszintes lépések végpontjainál lévő töréspontot megadni (az ábrában nullkörrel jelölve), hogy az útvonal meg legyen határozva. Ezek szerint a fenti 12 lépéses út (függőleges indulást feltételezve) megadható a következő szimbólumokkal Mivel a töréspontok száma jelen példában páros, azért az utolsó, vízszintes lépés végpontjában lévő töréspont, szükségképpen mindig a oszlopba kerül és így >><< helyett elég 7-et írni. Tehát a Az útvonalat részben megadó , , szimbólumok nem egyebek, mint a , , , , , elemeknek egy harmad osztályú kombinációja, az útvonalat másik részben megadó 3, 4, 6, 7 elemek pedig nem egyebek, mint a 2, 3, 4, 5, 6, 7 elemeknek egy negyed osztályú kombinációja. Minden útvonal ‐ a kezdőpontot és végpontot nem számítva ‐ kivétel nélkül 13 mezőn halad át, tehát ha 13-ból levonjuk a töréspontok számát (; jelen példánkban ), akkor a fennmaradó , jelen esetben mezőn helyezkedhetik el az számú, jelen esetben megálló. Tehát a megállókat megadó 3 mező: , , nem egyéb, mint az , , , , öt mezőnek egy harmadosztályú kombinációja. Mivel az itt szereplő 3 fajta kombinációs csoport mindegyikének bármely kombinációja kapcsolható egy másik kombinációs csoport bármely kombinációjával, azért az összes lehetséges utak számát megkapjuk, ha a 3 fajta kombinációknak számát összeszorozzuk. Ezek szerint tehát a 12 lépéses és 8 törésponttal bíró utak száma Általában, ha a lépés szám és a töréspontok száma páros , akkor Ha a töréspontok száma páratlan , akkor az utolsó töréspont (továbbra is függőleges kezdőlépést feltételezve) szükségképpen mindig egy függőleges lépés végpontja a 8. sorban. A függőleges lépések végpontjaiban lévő töréspontok száma tehát a vízszintes lépések végén lévő töréspontok száma pedig . Ez utóbbiakat megadó szimbólumok egyrészt a A nyert két képlet egyesíthető a jelölés bevezetésével (olvasd: egész része<< v.entier [antjé] ), amely az -ben foglalt legnagyobb egész számot jelenti. Ugyanis, ha páros, akkor Az összes lépéses utak számát, -et megkapjuk, ha rendre kiszámítjuk az utak számát , 2, 3, , töréspont esetén és az így nyert eredményeket összeadjuk. Tehát és így
b) I. megoldás: Ha 12 lépésben akarunk -ra jutni, akkor vagy kétszer kell 2 egységnyit lépni, vagy egyszer 3 egységnyit. Ha az utóbbi lépéseket , illetőleg , -mal jelöljük, akkor a következő elemek permutációjáról van szó:
II. megoldás: Alkalmazzuk az a) IV. megoldásánál nyert képletet: amiből c) I. megoldás: Egy irányban 2 lépést a másik irányban 3 lépést megtéve az Az első csoport minden sorát a második csoport minden sorával összekapcsolva és az így nyert 5 elemet esetről-esetre permutálva Egy irányban 1 lépést a másik irányban 4 lépést megtéve az Az utak száma ez esetben Tehát az összes utak száma II. megoldás: A a) IV. megoldásnál nyert képletet alkalmazva: és így |