Kezdőlap


Feladat:	415. matematika feladat	Korcsoport: 18-	Nehézségi fok: nehéz
Füzet:	1952/május, 143 - 146. oldal		PDF \| MathML
Témakör(ök):	Kocka, Határozott integrál, Hiperbola egyenlete, Térfogat, Hiperbola, mint kúpszelet, Feladat
Hivatkozás(ok):	Feladatok: 1951/december: 415. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Betűzés az ábra szerint.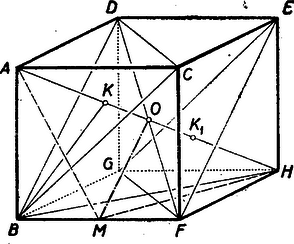

Mivel a kocka élhossza

1

, azért a lapátló

\sqrt[]{1^{2} + 1^{2}} = \sqrt[]{2}

és a testátló

\sqrt[]{1^{2} + {(\sqrt[]{2})}^{2}} = \sqrt[]{3}

.
Ha a kockát pl. az

A H

testátló körül forgatjuk, akkor az

A

pontból kiinduló

3

él (illetőleg a

3

él mindegyike külön-külön) egy forgáskúp testet ír le, melynek csúcspontja

A

, alapköre a

B C D

szabályos háromszög köré írt,

K

középpontú kör és magassága

m = A K

. Mivel a

B C D

szabályos háromszög oldalhossza

\sqrt[]{2}

, azért a köré írt kör sugara (a szabályos háromszög magasságának

\frac{2}{3}

-ad része)

r = \frac{2}{3} \cdot \frac{\sqrt[]{2}}{2} \sqrt[]{3} = \frac{\sqrt[]{6}}{3}

(Az

r = B K

távolság az

A B H

derékszögű háromszögből, az átfogóhoz tartozó magasságként is kiszámítható:

B K : A B = B H : A H

vagyis

r : 1 = \sqrt[]{2} : \sqrt[]{3}

, miből

r = \frac{\sqrt[]{2}}{\sqrt[]{3}} = \frac{\sqrt[]{6}}{\sqrt[]{3}})

. Az

m = A K

kúpmagasság az

A B H

derékszögű háromszögből számítható ki, mint az

A B

befogónak vetülete az

A H

átfogón. Tehát

A K : A B = A B : A H

, vagyis

m : 1 = 1 : \sqrt[]{3}

, miből

m = \frac{1}{\sqrt[]{3}} = \frac{\sqrt[]{3}}{3}

. A forgáskúp térfogata

\begin{matrix} V_{1} = \frac{1}{3} \cdot r^{2} π \cdot m = \frac{1}{3} \cdot {(\frac{\sqrt[]{6}}{3})}^{2} π \frac{\sqrt[]{3}}{3} = \frac{6 \sqrt[]{3}}{81} π = \frac{2 \sqrt[]{3}}{27} π \end{matrix}

Ugyanez áll természetesen a

H

csúcspontból kiinduló

3

kockaél által leírt forgáskúpra is, és így e két kúp köbtartalma

\begin{matrix} 2 V_{1} = \frac{4 \sqrt[]{3}}{27} π \end{matrix}

A kocka többi

6

éle (illetőleg e

6

él mindegyike) egy egyköpenyű forgáshiperboloidot ír le. Az él, mint szakasz, által leírt hiperboloidfelület is az él végpontjai által leírt két kör lapja által (e két körlap az előbbi két forgáskúp alapköre) határolt forgástest térfogatát:

V_{2}

-t integrálással számítjuk ki. Evégből helyezzük egész forgástestünk

A B E^{*}

H

meridiánját egy derékszögű koordináta rendszer síkjába úgy, hogy a kocka középpontja, vagyis az

A H

felezőpontja

O

az origóba kerül és az

A H

forgástengely az

x

tengellyel esik egybe. Akkor

y

a meridián szimmetria tengelye, melyen rajta van a hiperbola valós tengelye.

E^{*}

E

pontnak

180

fokos elforgatása. Mint láttuk

A K = H K_{1} = \frac{\sqrt[]{3}}{3}

és így

K K_{1} = \sqrt[]{3} - \frac{2 \sqrt[]{3}}{3} = \frac{\sqrt[]{3}}{3} = A K = H K_{1}

, vagyis a

K

és

K_{1}

pont az

A H

forgástengelyt

3

egyenlő részre osztja.

O K = O K_{1} = \frac{\sqrt[]{3}}{6}

. Jelöljük a hiperbola fél-valóstengelyét

O M_{0}

-val.

O M_{0}

nem egyéb, mint az

O

kockaközéppontnak távolsága az említett

6

él bármelyikétől pl.

B F

-től. E távolság azonos az

O

-nak a

B F

él felezőpontjától,

M

-től való távolságával, mert hiszen

O M ⊥ B F

. Az

O M

azonkívül, mint az

A M H

egyenlő szárú háromszög magassága, az

A H

-ra is merőleges. (A reálisták felismerik, hogy

O M

A H

forgástengely és a

B F

él normál-transzverzálisa.) Az

M O H

derékszögű háromszögből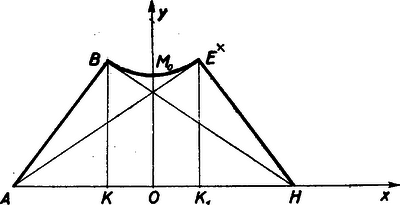

O M^{2} = A M^{2} - A O^{2}

, de

A M^{2} = 1 + {(\frac{1}{2})}^{2} = \frac{5}{4}

, és

A O^{2} = {(\frac{\sqrt[]{3}}{2})}^{2} = \frac{3}{4}

és így

O M^{2} = \frac{5}{4} - \frac{3}{4} = \frac{2}{4} = \frac{1}{2}

, vagyis

O M = \frac{1}{\sqrt[]{2}} = \frac{\sqrt[]{2}}{2}

(Azok, akik ábrázoló geometriát tanultak, erre az eredményre úgy is juthatnak, visszaemlékezve a kocka ábrázolására, ha meggondolják, hogy a kockát az

A H

csúcstengellyel párhuzamos irányból vetítve a csúcstengelyre merőleges síkra, a hiperboloidot leíró

6

él vetülete szabályos hatszög, amely köré írt kör sugara a fenti

r = \frac{\sqrt[]{3}}{6}

. Az

O M

sugarú kör egybevágó vetületével, amely e szabályos hatszögbe írt kör és így sugara

\begin{matrix} O M = O M_{0} = \frac{1}{2} r \sqrt[]{3} = \frac{1}{2} \cdot \frac{\sqrt[]{6}}{3} \cdot \sqrt[]{3} = \frac{\sqrt[]{18}}{6} = \frac{3 \sqrt[]{2}}{6} = \frac{\sqrt[]{2}}{2}) . \end{matrix}

A meridián síkban fekvő hiperbola egyenlete:

\frac{y^{2}}{a^{2}} - \frac{x^{2}}{b^{2}} = 1

, ahol

a

jelenti a valóstengely felét, vagyis

a = O M_{0} = \frac{\sqrt[]{2}}{2}

. Ezt az értéket behelyettesítve, nyerjük

\begin{matrix} 2 y^{2} - \frac{x^{2}}{b^{2}} = 1 \end{matrix}

b^{2}

meghatározása úgy történik, hogy a hiperbola egy pontjának, pl. a

B

pont koordinátáit:

(- \frac{\sqrt[]{3}}{6}, \frac{\sqrt[]{6}}{3})

behelyettesítjük a hiperbola egyenletébe:

\begin{matrix} 2 \cdot \frac{2}{3} - \frac{1}{12 b^{2}} = 1, \end{matrix}

miből

\begin{matrix} \frac{1}{b^{2}} = (\frac{4}{3} - 1) \cdot 12 = 4. \end{matrix}

Tehát a hiperbola egyenlete

\begin{matrix} 2 y^{2} - 4 x^{2} = 1, \end{matrix}

vagyis

\begin{matrix} y^{2} = \frac{4 x^{2} + 1}{2} = 2 x^{2} + \frac{1}{2} \end{matrix}

A forgáshiperboloid test térfogata:

\begin{matrix} V_{2} = π \int_{- \frac{\sqrt[]{3}}{6}}^{\frac{\sqrt[]{3}}{6}} y^{2} d x = 2 π \int_{0}^{\frac{\sqrt[]{3}}{6}} y^{2} d x = 2 π \int_{0}^{\frac{\sqrt[]{3}}{6}} (2 x^{2} + \frac{1}{2}) d x = \\ = 2 π {[\frac{2}{3} x^{3} + \frac{1}{2} x]}_{0}^{\frac{\sqrt[]{3}}{6}} = 2 π (\frac{2}{3} \cdot \frac{3 \sqrt[]{3}}{216} + \frac{1}{2} \cdot \frac{\sqrt[]{3}}{6}) = 2 π (\frac{\sqrt[]{3}}{108} + \frac{\sqrt[]{3}}{12}) = \\ = 2 π \frac{\sqrt[]{3} + 9 \sqrt[]{3}}{108} = 2 π \frac{10 \sqrt[]{3}}{108} = \frac{5 \sqrt[]{3}}{27} π . \end{matrix}

Az egész forgástest térfogata tehát

\begin{matrix} V = 2 V_{1} + V_{2} = \frac{4 \sqrt[]{3}}{27} π + \frac{5 \sqrt[]{3}}{27} π = \frac{9 \sqrt[]{3}}{27} π = \frac{\sqrt[]{3}}{3} π . \end{matrix}

Megjegyzés: Forgástestünk térfogata éppen fele azon forgáshenger térfogatának, melynek sugara

B K = r = \frac{\sqrt[]{6}}{3}

és magassága

A H = \sqrt[]{3}

. (A forgástest köré írt henger.)