Kezdőlap


Feladat:	408. matematika feladat	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Babics B. , Balatoni F. , Csaba L. , Csom Gy. , Darvas I. , Durst E. , Főző Éva , Grätzer Gy. , Horváth J. , Kántor S. , Keszei J. , Németh Gy. , Papp I. , Pergel J. , Rejtő Péter , Révész P. , Schmidt E. , Schmidt Ibolya , Szabó D. , Szabó J. , Szabó Magdolna , Szilárd M. , Tahy P. , Tilesch F. , Vértes A. , Vida Piroska , Zatykó L.. , Zobor E.
Füzet:	1952/május, 136 - 137. oldal		PDF \| MathML
Témakör(ök):	Háromszögek hasonlósága, Hossz, kerület, Négyzetek, Feladat
Hivatkozás(ok):	Feladatok: 1951/december: 408. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Megjegyzés. Mielőtt a megoldásra rátérnénk, vegyük észre, hogy az $A M$ egyenes a négyzetet egy trapézra és egy háromszögre bontja és ha megállapodunk abban, hogy a háromszög csúcsát jelöljük $D$ -vel, ezzel biztosítjuk, hogy a tételt az első megfogalmazásban mondjuk ki, tehát $B N + D M = A M$ , így a másik megfogalmazással nem is kell törődnünk.

I. megoldás. Mérjük vissza

A M

egyenesen

M

pontból az

M D

távolságot, nyerjük a

K

pontot, ha sikerül bebizonyítanunk, hogy

K A = N B

, ezzel tételünket igazoltuk.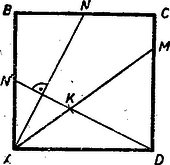

Kössük össze a

D

pontot

K

-val, messe ez az egyenes az

A B

oldalt

N'

pontban.
A szerkesztés szerint az

A K N'_{▵}

egyenlő szárú (hiszen

D K M_{▵}

-höz hasonló), ezért

A N

szögfelező merőleges

N' D

-re. Ebből az következik, hogy

\begin{matrix} A B N_{▵} ≅ D A N'_{▵}, \end{matrix}

\begin{matrix} N B = N' A = K A \end{matrix}

(a legutolsó egyenlőség abból folyik, hogy

A K N'_{▵}

egyenlő szárú)

Rejtő Péter (Bp. Ref. gimn. IV. o. t.)

II. megoldás. Mérjük rá a

B N

távolságot

D

-től kezdve

C D

meghosszabbítására, nyerjük az

N'

pontot, melyet összekötünk

A

-val. Tételünket bebizonyítottuk, ha sikerül kimutatni, hogy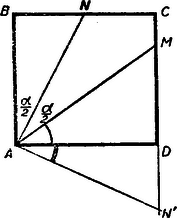

M A = M N'

Jelöljük az elfelezett szöget

α

-val, ekkor az

A

csúcsnál egy ívvel megjelölt szög

90^{\circ} - α

a mellette fekvő két íves szög pedig

\frac{α}{2}

miután

A B N_{▵} ≅ A D N'_{▵}

. Ugyanezért az

N'

-nél fekvő szög egyenlő az

N

-nél fekvő hegyesszöggel, tehát

90^{\circ} - \frac{α}{2} .

De ennyi az

A

-nál fekvő egyíves és kétíves szög összege is

(90 - α + \frac{α}{2} = 90 - \frac{α}{2})

tehát

A M N'_{▵}

egyenlő szárú és

M A = M N'

Schmidt Ibolya (Kaposvár, Munkácsy lg. III. o. t.)