Feladat:	370. matematika feladat	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Kovács László ,  Pap A. ,  Schmidt E. ,  Veszprémi áll. ált.g. mat. szakköre
Füzet:	1952/április, 85 - 86. oldal		PDF  |  MathML
Témakör(ök):	Háromszögek nevezetes tételei, Körülírt kör, Húrnégyszögek, Feladat
Hivatkozás(ok):	Feladatok: 1951/november: 370. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.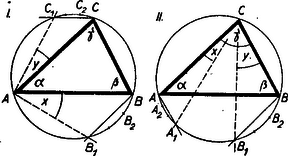   Legyen a $B_{1}AB\sphericalangle =x$ és $C_{1}AC\sphericalangle =y$, akkor $B_{2}AB\sphericalangle =\frac{x}{3}$ és $C_{2}AC\sphericalangle =\frac{y}{3}$, mivel az ív harmadrészéhez a kerületi szög harmadrésze tartozik. Az $ABC{C}_1$ négyszög trapéz, mert a feltétel szerint $C{C}_1\parallel AB$, továbbá mivel húrnégyszög, azért egyenlőszárú trapéz. Így $C_{1}AB\sphericalangle =CBA\sphericalangle$ vagyis $\alpha +y=\beta$, miből $y=\beta -\alpha$. Hasonlóképpen $\alpha +x=\gamma$, miből $x=\gamma -\alpha$. ${\displaystyle \begin{array}{c}\hfill {\displaystyle \text{A}{B}_{2}A{C}_2\sphericalangle =\frac{x}{3}+\frac{y}{3}+\alpha =\frac{\left(\gamma -\alpha \right)+\left(\beta -\alpha \right)+3\alpha }{3}=\frac{\alpha +\beta +\gamma }{3}=\frac{{180}^{\circ }}{3}={60}^{\circ }\mathrm{.}}\hfill \end{array}}$ Hasonlóképpen