Kezdőlap


Feladat:	369. matematika feladat	Korcsoport: 16-17	Nehézségi fok: könnyű
Megoldó(k):	Balázs B. , Blaskó F. , Dancs I. , Durst E. , Hraskó P. , Jaky P. , Kántor S. , Kovács L. , Marik M. , Molnár T. , Németh Gy. , Papp I. , Pataki K. , Schmidt E. , Szabó D. , Szabó J. , Tilesch F. , Tisovszky J. , Veszprémi áll. ált. g. mat. szakköre , Villányi O. , Zatykó L.
Füzet:	1952/április, 84 - 85. oldal		PDF \| MathML
Témakör(ök):	Háromszögek hasonlósága, Trapézok, Feladat
Hivatkozás(ok):	Feladatok: 1951/november: 369. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Legyenek a trapéz csúcspontjai $A$ , $B$ , $C$ és $D$ . A $C D$ párhuzamos oldal felezőpontja $E$ , az $A E$ és $B D$ egyenesek metszéspontja $P$ , az $A C$ és $B E$ metszéspontja $Q$ . A $P Q$ egyenesnek metszéspontjai az $A D$ , ill. $B C$ szárakkal legyenek $R$ és $S$ . Bebizonyítandó, hogy 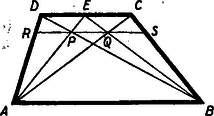$R P = P Q = Q S$ .

Először azt bizonyítjuk, hogy a

P Q

egyenes párhuzamos a trapéz párhuzamos oldalaival.

\begin{matrix} A B P ▵ \sim E D P ▵, \end{matrix}

mert a szögek egyenlők. Ebből következik, hogy

\begin{matrix} A P : P E = A B : E D, \end{matrix}

hasonlóképpen nyerjük, az

A Q B

és

C Q E

hasonló háromszögekből, hogy

\begin{matrix} B Q : Q E = A B : E C . \end{matrix}

Mivel

E D = E C

, azért

B Q : Q E = A P : P E

. Ebből

(B Q + Q E) : Q E = (A P + P E) : P E

, vagyis

\begin{matrix} B E : Q E = A E : P E . \end{matrix}

A B E

háromszögben és a

P Q E

háromszögben két-két oldal aránya egyenlő, a két oldal által bezárt szög közös, tehát e két háromszög hasonló és így

P Q

és

A B

párhuzamosak.
Az

A C D

háromszögnek

A E

súlyvonala, s így felezi a

C D

oldallal párhuzamos

R Q

szakaszt is:

R P = P Q

. Hasonlóképpen a

B D C

háromszögből

P Q = Q S

. Összevetve

R P = P Q = Q S

, amit bizonyítani akartunk.